
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вращения направлены в одну сторону
Этот случай имеет место, например, в планетарном редукторе, в котором зубчатое колесо 2 (рис.2.38) вращается относительно оси водила BB1 с угловой скоростью w2 (относительное вращение) при этом водило 1, в свою очередь, вращается относительно неподвижной оси AA1 с угловой скоростью w1 (переносное вращение). Очевидно, точка A тела 2 участвует только в относительном движении, а точка B – только в переносном движении.
 Из рассмотрения чертежа следует, что результирующее движение тела 2 будет плоским, следовательно для него можно найти МЦС.
Из рассмотрения чертежа следует, что результирующее движение тела 2 будет плоским, следовательно для него можно найти МЦС.
Для определения характеристик результирующего движения найдем скорости точек А и В:
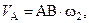
| (2.47) |

|
или по свойству МЦС (точка C)

| (2.48) |

|
Найдем из уравнения (2.48) угловую скорость мгновенного вращения
 
| (2.49) |

|
Решим совместно (2.47) и (2.49):
 . .
| (2.50) |
Угловая скорость мгновенного вращения в данном случае равна сумме угловых скоростей относительного и переносного вращений. Этот результат можно было бы получить при сложении векторов угловых скоростей относительного и переносного вращений по правилу сложения параллельных сил.
Таким образом, результирующее движение тела можно изучать на основе всех уравнений, полученных для плоского движения.
9.1.2 Вращения направлены в противоположные
стороны
Как и в предыдущем случае результирующее движение будет плоским. Пусть для определенности  . Тогда МЦС (точка C) найдется так, как показано на рис. 2.39. Следовательно
. Тогда МЦС (точка C) найдется так, как показано на рис. 2.39. Следовательно

 то есть мгновенная угловая скорость равна разности угловых скоростей переносного и относительного движений.
то есть мгновенная угловая скорость равна разности угловых скоростей переносного и относительного движений.
 . .
| (2.51) |
Из анализа (2.51) следует, что в случае, если переносная и относительная угловые скорости равны по величине, то мгновенная угловая скорость  , т.е. в этом случае тело совершает мгновенно поступательное движение.
, т.е. в этом случае тело совершает мгновенно поступательное движение.
Примером такого движения может служить движение педали велосипеда, которая вращается с относительной угловой скоростью  относительно кривошипа, который в свою очередь вращается с переносной угловой скоростью
относительно кривошипа, который в свою очередь вращается с переносной угловой скоростью  относительно рамы велосипеда (рис. 2.40).
относительно рамы велосипеда (рис. 2.40).
Дата добавления: 2015-04-15; просмотров: 216; Мы поможем в написании вашей работы!; Нарушение авторских прав |