Мгновенный центр скоростей.

Теорема:Если тело совершает плоское движение, то всегда имеется такая точка, жестко связанная с телом, скорость которой в данный момент времени равна нулю. Такая точка называется мгновенным центром скоростей (МЦС).

МЦС лежит на пересечении перпендикуляров к векторам скоростей двух каких-нибудь точек тела (рис. 2.26).

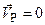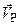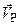Докажем, что скорость точки Р(МЦС) . Предположим, что . Тогда по теореме о проекциях скоростей точек на прямую их соединяющую вектор должен быть перпендикулярен AP, так как . С другой стороны должен быть перпендикулярен BP, так как 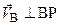. Получаем противоречие: вектор 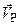должен быть одновременно перпендикулярен непараллельным отрезкам AP и BP, что невозможно. Следовательно 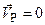, что и требовалось доказать.

Свойства МЦС.

Запишем уравнения для определения скоростей точек А и В, приняв МЦС за полюс:

,

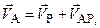
(2.31)

Очевидно , , откуда

(2.32)

Из (2.31) и (2.32) вытекают следующие свойства МЦС:

1) Скорости точек тела при плоском движении прямопропорциональны их расстояниям до МЦС.

2) Скорости точек перпендикулярны отрезкам, соединяющим эти точки с МЦС.

Частные случаи определения МЦС.

1. Скорости точек A и B тела составляют одинаковый угол с прямой AB (рис. 2.27). Очевидно при этом , , то есть в этом случае тело совершает мгновенно поступательные движения.

2. Скорости точек A и B тела перпендикулярны отрезку AB и не равны. На основе (2.32) МЦС находится так, как показано на рис. 2.28.

3. Скорости точек А и В перпендикулярны отрезку AB и направлены в противоположные стороны. МЦС определяется так, как показано на рис. 2.29.

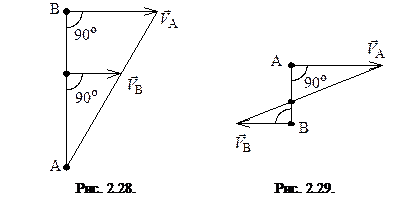4. Колесо катится без скольжения прямолинейно. В данном случае МЦС находится в точке касания А (рис. 2.30).