Мгновенный центр ускорений

При плоском движении тела всегда имеется точка, жестко связанная с телом, ускорение которой в данный момент времени равно нулю. Такая точка называется мгновенным центром ускорений (МЦУ).

Пусть тело совершает плоское движение, при этом известны ускорение произвольной точки A, а также угловая скорость w и угловое ускорение e (рис. 2.32).

Для нахождения МЦУ необходимо:

1) Найти угол m из выражения ;

2) Отложить от вектора полупрямую AB под углом m в сторону направления углового ускорения e;

3) Отложить на полупрямой AB отрезок

.

(2.37)

Найденная точка Q и будет МЦУ.

Свойства МЦУ: 1) ускорения всех точек тела составляют один и тот же угол m с отрезками, соединяющими их с МЦУ; 2) модули ускорений всех точек тела пропорциональны их расстоянию до МЦУ.

Пример 2.12. Определить величину и направление ускорения точки C шатуна AB кривошипно-ползунного механизма, если кривошип 0A вращается с постоянной угловой скоростью ; ; (рис. 2.33).

Для решения задачи найдем МЦУ шатуна AB. Так как , то угловая скорость шатуна AB для указанного положения . Тогда и .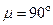

При 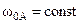ускорение точки A направлено к центру вращения кривошипа 0A. Следовательно МЦУ для шатуна AB находится на линии . С другой стороны, ускорение ползуна B направлено по линии 0B, поэтому отрезок BD, соединяющий точку B с МЦУ должен быть перпендикулярен 0B. Пересечение линий AE и BD определяет положение точки Q – МЦУ для шатуна AB. По свойству МЦУ вектор точки ускорения точки C 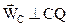, а его модуль найдется из пропорции

.