Определение абсолютной скорости

Очевидно, вектор абсолютного перемещения 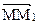можно представить как сумму векторов относительного и переносного перемещений точки M:

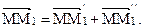
(2.38)

Разделив равенство (2.38) на и переходя к пределу, получим:

или

(2.39)

Уравнение (2.39) выражает следующую теорему: абсолютная скорость точки при сложном движении ровна геометрической сумме ее относительной и переносной скоростей.

Векторы , и направлены по касательным к соответствующим траекториям (рис. 2.35).

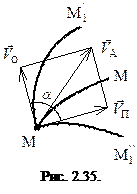В общем случае модуль абсолютной скорости находится из уравнения

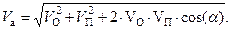
(2.40)

Пример2.13. Определить абсолютную скорость колечка M, которое движется вдоль стержня ОА по закону см, при этом стержень ОА вращается в соответствии с уравнением 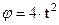, рад (рис. 2.36). Движение колечка по стержню будем считать относительным. Тогда относительная скорость 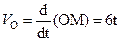, см/с.

Для определения переносной скорости мысленно остановим движение колечка по стержню, тогда точка М будет двигаться по окружности радиуса ОМ. Следовательно или 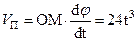, см/с.

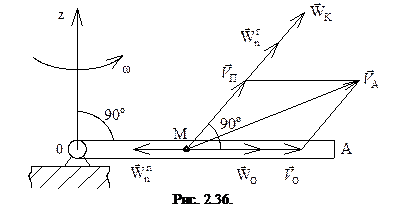Вектор переносной скорости направлен по касательной к окружности радиуса OM и тогда

, см/с.