Неоднородные системы линейных алгебраических уравнений (СЛАУ).

Исследовать систему и в случае совместности найти ее решения.

1) , 2) ,

3) 4) .

Исследование системы будем проводить в следующем порядке:

1) Составим расширенную матрицу системы (АIb) и с помощью элементарных преобразований получим ее приведенную форму.

2) Найдем ранги r(A), r(AIb) и по теореме Кронекера-Капелли сделаем выводы.

Если система неопределена, то переходим к пункту 3 и продолжим изучение.

3) По приведенной матрице А восстановим однородную систему уравнений и найдем ее множество решений X₀₀.

4) По приведенной расширенной матрице (АIb) восстановим неоднородную систему уравнений и, положив параметрические неизвестные равными, например, нулю, найдем частное решение X_ч.н..

5) Общее решение неоднородной системы представляет собой сумму общего однородного и частного неоднородного решений, то есть X_о.н.=X_о.о+X_ч.н..

1)

_1. (AIb)= 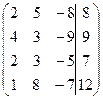~^C₁^-C₄ ~ ^C₂^-4C_1, ^C₃^-2C_1, ^C₄^-C_1,

~ ~^C₂^{:5, C}₃^:3 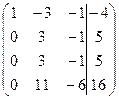~ ^C₃^-C_2, ^C₄^-4C₂ ~ ~ ^C₂^+2C₄ ~ ^C₁^+3C_2, ^C₃^+C₂ ~ ~^C₃^(-7) ~ ^C₁^+16C_3, ^C₂^+5C₃ ~ _.

2. Определитель =1 0 является для матриц А и (AIb) базисным минором, поэтому r(A)=r(AIb)=3 и по теореме Кронекера-Капелли исходная система уравнений совместна. Так как число неизвестных n=3 совпадает с рангом r(AIb), то система имеет единственное решение, то есть определена. Это решение найдем восстановив систему по приведенной матрице (AIb):

.

2) 1.

(AIb)= ~^C₂^+C₁ , ^C₃^-2C₁ ~ ^C₂^+C₃ , ^C₃^(-1)

~ ~^C₁^-2C₂ , ^C₃^-3C₂ ~^C₁^+C₃ .

2. Матрица А имеет базисный минор , следовательно, r(A)=3. Ранг расширенной матрицы также равен 3, так как рассмотренный выше минор является базисным минором и для матрицы (АIb).

Итак, по теореме Кронекера-Капелли исходная система совместна. Поскольку число неизвестных системы п=4 больше, чем r(AIb), то система имеет бесконечно много решений, то есть является неопределенной.

3. Однородная система имеет вид:

.

Так как r(A)=3, n=4, то размерность пространства решений однородной системы L=r(A)-n=4-3=1 и существует только один базисный вектор ₁. Координаты этого вектора получаются из равенств:

,

если положить в них параметрическую переменную x₄ равную 1. Имеем,

и ₁= , X₀₀=C , C R.

4. Неоднородная система имеет вид:

. Полагая здесь X₄=0, получим: и X_ч.н.= .

5. Общее решение исходной системы имеет вид:

X_{о. н.}=C + , C R.

3) 1. (AIb)= ~^C₂^-2C₁ , ^C₃^-C₁ ~ ^C₂ ^(-1), ^C₃^+C₂ ~ 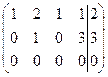~ ^C₁^-2C_{1 .}

2. Определитель =1 0 является для матриц А и (АIb) базисным минором, поэтому r(A)=r(AIb)=2. По теореме Кронекера-Капелли система уравнений совместна, и так как число неизвестных п=4 больше ранга r(AIb), то система неопределена.

3. Однородная система имеет вид

или .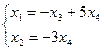

Так как r(A)=2, п=4, то пространство решений однородной системы имеет размерность L=4-2=2 и содержит два базисных вектора ₁, ₂. Полагая в последней системе уравнений параметрические неизвестные x₃=1, x₄=0, получим

, ₁= , и x₃=0, x₄=1, получим , ₂= .

Общее решение однородной системы: X₀₀=С₁ +С₂ , C₁,C₂ R.

4. Неоднородная система имеет вид

. Полагая здесь x₃=x₄=0, получим и частное решение X_x.н.= .

5. Общее решение исходной системы:

X_o.н.=C₁ +С₂ + , C₁,C₂ R.

4) 1 (AIb)= ~ ^C₁^+C₂ , ^C₃^-C₂ 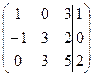~ ^C₂^+C₁ ~ ~

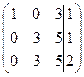~ ^C₃^-C₂ .

2. Матрица А~ ~ имеет базисный минор второго порядка, следовательно, r(A)=2. Ранг расширенной матрицы (AIb)= равен трем, поскольку ее минор 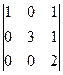=6 0.

Итак, r(A) r(AIb), стало быть, по теореме Кронекера-Капелли исследуемая система уравнений не имеет решений, то есть несовместна.