
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задачи на тему “Системы линейных алгебраических уравнений”.
Определить размерность пространства решений, найти базис (фундаментальную систему решений) и общее решение следующих систем:
1) 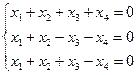 , 2)
, 2) 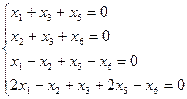 ,
,
3)  , 4)
, 4) 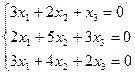 .
.
Для каждого из рассматриваемых случаев составим матрицу системы, с помощью элементарных операций преобразуем ее к приведенной форме, то есть, последовательно сформируем на главной (или смещенной) диагонали единицы, а выше и ниже диагонали нули. После чего, определим ранг и найдем решение системы.
 1) А=
1) А=  ~C2-C1, C3-C1
~C2-C1, C3-C1  ~C2;(-2), C3(-2) ~
~C2;(-2), C3(-2) ~ 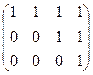 .
.
Вторым элементом главной диагонали является ноль, а нам нужен не нулевой элемент, чтобы получить на диагонали единицу, поэтому здесь необходимо рассмотреть смещенную диагональ. Элементарными преобразованиями С1-С2 и С2-С3 преобразуем эту матрицу к приведенной форме:
A~  .
.
Отсюда, ранг исследуемой матрицы А: r(A)=3.
Пространство решений  имеет размерность L=n-r=4-3=1,где n=4-число неизвестных системы, и содержит один базисный вектор
имеет размерность L=n-r=4-3=1,где n=4-число неизвестных системы, и содержит один базисный вектор  . Чтобы найти базисный вектор, восстановим по приведенной матрице систему:
. Чтобы найти базисный вектор, восстановим по приведенной матрице систему:
 ,
,
и выразим базисные неизвестные x1, x3, x4, соответствующие элементам смещенной диагонали, через параметрическое неизвестное x2;
 .
.
В полученной системе положим x2=1, будем иметь:
 =
=  ,
,  .
.
|
|
2) A=  ~ C3-C1, C4-2C1
~ C3-C1, C4-2C1  ~
~
~C3+C2, C4+C2  ~
~  .
.
Таким образом, ранг матрицы А: r(A)=2, размерность пространства решений L=6-2=4.
Восстановим по последней матрице систему:
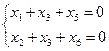
и выразим базисные неизвестные x1, x2 через параметрические x3, x4, x5, x6:
 .
.
Найдем теперь фундаментальную систему решений, состоящую из четырех(L=4) векторов, полагая,
для  1: x3=1, x4=0, x5=0, x6=0;
1: x3=1, x4=0, x5=0, x6=0;
для  2: x3=0, x4=1, x5=0, x6=0;
2: x3=0, x4=1, x5=0, x6=0;
для  3: x3=0, x4=0, x5=1, x6=0;
3: x3=0, x4=0, x5=1, x6=0;
для  4: x3=0, x4=0, x5=0, x6=1,
4: x3=0, x4=0, x5=0, x6=1,
имеем:
 1=
1=  ,
,  2=
2= 
 3=
3= 
 4=
4=  и
и  =C1
=C1  +C2
+C2  +C3
+C3  +C4
+C4  ; C1 ,C2, C3, C4
; C1 ,C2, C3, C4  R.
R.
|
|
3) A=  ~C2+C1
~C2+C1  ~
~ 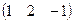 ,
,
r(A)=1, L=3-1=2.
Восстановим систему и выразим единственную базисную неизвестную x1 через параметрические x2, x3;
X1=-2x2+x3.
Теперь полагая
для  1: x2=1, x3=0
1: x2=1, x3=0
для  2: x2=0, x3=1, получим:
2: x2=0, x3=1, получим:
 1=
1= 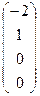 ,
,  2=
2= 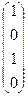 и
и 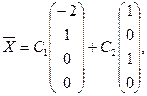 C1,C2
C1,C2  R.
R.
| |||
| |||
4) A=  ~ C1-C2, C3-C2
~ C1-C2, C3-C2  ~ C2-2C1, C3-C1 ~
~ C2-2C1, C3-C1 ~  ~C2-5C3 ~
~C2-5C3 ~ 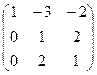 ~ C1+3C2, C3-2C2
~ C1+3C2, C3-2C2  ~C3:(-3) ~
~C3:(-3) ~  ~ C1-4C3, C2-2C3 ~
~ C1-4C3, C2-2C3 ~  .
.
| Ранг матрицы А однородной системы r(A)=3. Пространство решений имеет размерность L=3-3=0 и поэтому не содержит базисных векторов и состоит только из нулевого вектора: |
 = =  . . 
|
Дата добавления: 2015-04-15; просмотров: 249; Мы поможем в написании вашей работы!; Нарушение авторских прав |