Множество решений однородной системы.

Рассмотрим однородную систему m уравнений с n неизвестными:

(1).

Однородная система линейных уравнений всегда совместна, т.к. одним из решений является тривиальное уравнение (0,0,….0)

Предложение. Если однородная система (1) имеет два решения X= (х_1,х₂,…х_n) и Y=(y_1, y_2,…. y_n ), то любая линейная комбинация решений Z также решение: Z=a .

Рассмотрим матрицу системы (1)

A=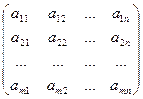

Применяя элементарные преобразования строк приведем матрицу А к упрощенному виду:

Отсюда r(A)= r и D= 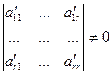базисный минор.

Данная нам система линейных уравнений перейдет в эквивалентную ей систему из r линейно независимых уравнений:

(2)

В левых частях равенств мы оставили неизвестные, соответствующие столбцам базисного минора , так называемые базисные неизвестные. Остальные неизвестные – называемые параметрическими – перенесены в правые части равенств.

Всего параметрических неизвестных n – r.

Тогда решая систему (2), например, по формулам Крамера, получили:

(3).

Параметрическим неизвестным задаем значения по схеме:

1) x_r+1=1, x_r+2=0, …, x_n=0,

2) x_r+1=0, x_r+2=1, …, x_n=0, (4)

… … …

n-r) x_r+1=0, x_r+2=0, … x_n=1.

Для каждой совокупности значений параметрических неизвестных найдем из системы (3) соответствующие базисные неизвестные:

1) x₁₁, x_{12, …,} x_1r,

2) x₂₁, x₂₂, …, x_2r,

… … …

n-r) x_{n-r 1}, x_{n-r 2}, …, x_{n-r r.}

Получаем n – r решений системы (1):

, , …, (5).

Эти решения линейно независимы, т.к. матрица из их столбцов имеет минор порядка n-r, равный единице.

Совокупность решений (5) называется нормальной фундаментальной системой решений.

Тогда любое решение линейной однородной системы представляет собой линейную комбинацию нормальной фундаментальной системы решений:

, где с₁, c₂, …,c_n-r –произвольные постоянные.