Метод Гаусса.

С помощью элементарных преобразований строк приведем матрицу размера n´n к треугольному виду:

Затем начинается, так называемый “обратный ход”: из последнего уравнения системы определяется x_n , подставляем это значение в предпоследнее уравнение, определяем x_n-1 и так далее, пока из первого уравнения не определим x₁.

Пример.Дана система:

Найти решение: 1. по формулам Крамера,

2. методом обратной матрицы ,

3. методом Гаусса.

Решение:1. по формулам Крамера:

D=det(A)= =1 -2 -1 =-18 ¹0.

Dx₁= = -3 -2 -1 =-18 , x₁= =1.

Dx₂= =1 +3 -1 =18 , x₂= = -1.

Dx₃= =1 -2 -3 = -36 , x₂= = 2.

Ответ:{1; -1;2}.

2. методом обратной матрицы.

D=det(A)= = -18 .

Так как det(A)¹0, то по теореме об обратной матрице, определена.

Найдем алгебраические дополнения соответствующих элементов определителя det(A):

A11= = -5	A21= - =-7	A31= =1
A12=- = -3	A22= =3	A32=- = -3
A13= =7	A23=- = -1	A33= = -5

Строим союзную матрицу :

= .

Следовательно, =

Итак, решением системы будет

X=A^-1B= = = 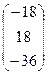, отсюда x₁=1, x₂=-1, x₃=2.

3. методом Гаусса.

Выпишем расширенную матрицу системы:

C= ~^C₂^-2C₁, ^C₃^-C₁ ~^C₂^+5C₃ ~^C₃^:18

Получаем систему треугольного вида:

x₁ + 2x₂ – x₃ = -3

-5x₂ + 3x₃ = 11

x₃ = 2

Отсюда x₃=2

-5x₂+6=11 Þ x₂= -1,

x₁+2x₂-x₃= -3 Þx₁-2-2=-3, x₁=1.

Ответ:{1; -1;2}

Замечание: C помощью элементарных преобразований, матрицу А можно привести к диагональному виду, а затем к единичной матрице.

Продолжим преобразование матрицы С:

~^C₁^+C₃, ^C₂^-3C₃ 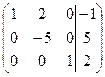~^C₂^:(-5) ~^C₁^-2C₂ .

Отсюда x₁=1, x₂=-1, x₃=2.