Лекция 4. Поверхности второго порядка.

1) Уравнение сферы с центром в точке С(a,b,c) радиуса R:

(x-a)²+(y-b)²+(z-c)²=R².

Особенностью уравнения сферы является то, что коэффициенты при квадратах неизвестных равны между собой. Центр сферы С(а;b;с) и R-радиус.

2) Трехосный эллипсоид определяется уравнением:

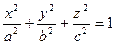
Величины a,b,c суть полуоси эллипсоида. Если все они различны, то эллипсоид называется трехосным. В случае, если какие-нибудь две из них равны между собой, эллипсоид является поверхностью вращения. Если, например, а=в, то осью вращения будет OZ.

3) Гиперболоиды.

Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяется уравнением:

a) (1) -однополостный гиперболоид.

b) (2) - двуполостный гиперболоид.

Величины a,b,c называются полуосями гиперболоида.

Для вычерчивания поверхностей второго порядка применяется метод сечения поверхности координатными плоскостями или плоскостями, параллельными координатным плоскостям:

a) однополосный гиперболоид:

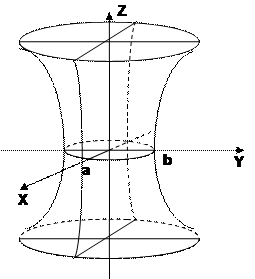1. Проведем сечение плоскостью z=0. В сечении получим горловой эллипс

.

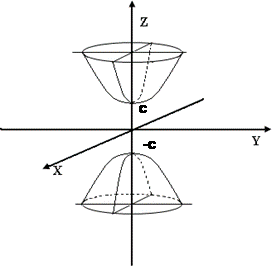2. Положим x=0, тогда в сечении получим гиперболу 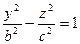с вещественной осью OY и мнимой осью OZ.

По аналогии строятся остальные сечения.

b) двуполостный гиперболоид:

4) Параболоиды.

Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями:

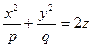(3) - эллиптический параболоид и

(4) - гиперболический параболоид,

при этом p и q – положительные числа, называемые параметрами параболоида.

В случае, когда p=q параболоид (3) является поверхностью вращения.

Вычертим параболоиды, используя метод сечения координатными плоскостями и плоскостями, параллельными координатным плоскостям:

a) эллиптический параболоид: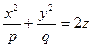

.

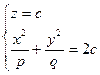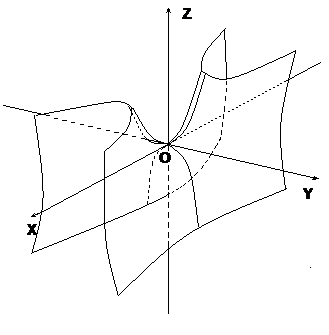b) гиперболический параболоид (седлообразная поверхность) .

Будем изображать эту поверхность в левой системе координат (поменяем оси OX и OY).

Гиперболический параболоид может быть получен путем параллельного перемещения параболы, представляющей собой сечение плоскостью Oxz (Oyz), когда ее вершина движется вдоль параболы, являющейся сечением параболоида плоскостью Oxz (Oyz).

5)

6) Эллиптический конус

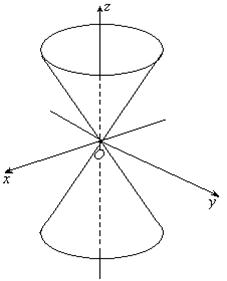Поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение

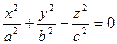, называется эллиптическим конусом или конусом второго порядка.

Конус состоит из прямых линий, проходящих через начало координат. Сечение конуса плоскостями z=a представляет собой эллипсы: .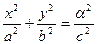

7) Цилиндры.

Цилиндрической поверхностью, или цилиндром, называется поверхность, которая получается при перемещении прямой (образующей) параллельно самой себе вдоль некоторой кривой(направляющей). Если образующая перемещается параллельно одной из осей координат, то цилиндр называется прямым. В уравнении прямого цилиндра отсутствует одна из координат. Название цилиндра определяется названием направляющей линии и образующая параллельна оси, одноименной с отсутствующей координатой.

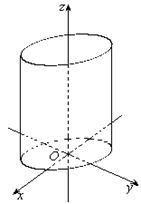
1. Эллиптический цилиндр:

.

Если, в частности, a=b, то данное уравнение является уравнением кругового цилиндра.

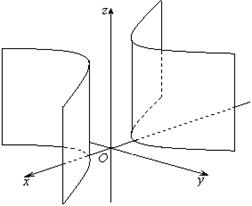
1. Гиперболический цилиндр:

.

Направляющей линией является гипербола с вещественной осью ОХ.

2. Параболический цилиндр:

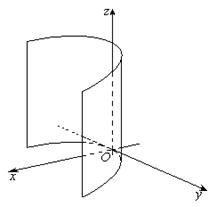у²=2px

Направляющей линией является парабола.

3. Поверхности вращения.

Пусть дана линяя 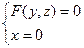и пусть она вращается вокруг оси OY, тогда уравнение поверхности вращения получается по следующему правилу: координата, одноименная с осью вращения остается в уравнении линии без изменения, а вторая координата заменяется на корень квадратный из суммы квадратов оставшихся координат. Так в нашем случае y~y, z~ 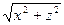и уравнение поверхности вращения F(y, 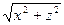)=0.

Например: линия у²=2px вращается вокруг оси OX. Уравнение соответствующей поверхности вращения будет y²+z²=2px – параболоид вращения вокруг оси OX.