Гипербола. Гиперболой называется множество точек плоскости, разность расстояний которых до двух данных точек, называемых фокусами гиперболы

Гиперболой называется множество точек плоскости, разность расстояний которых до двух данных точек, называемых фокусами гиперболы, постоянна и равна ±2а.

Фокальная ось гиперболы F₂ F₁ = 2c; r₁ , r₂ – фокальные радиусы гиперболы,

соответствующие точке М(х,у). r₂ – r₁ = ± 2а; 2с > 2а. с>а ( по свойству сторон треугольника)

Каноническое уравнение гиперболы

.

Обозначим с²-a²=b², тогда уравнение гиперболы примет вид:

.

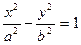Вершины гиперболы: А₁(а;о) А₂(-а,о) – вещественные вершины;

В₁(о;b) В₂(о;-b) – мнимые вершины.

Прямые y= являются асимптотами гиперболы.

Гипербола состоит из двух несмыкающихся ветвей, лежащих в углах между прямыми у = , y= и неограниченно приближающихся к этим прямым. А₁ вещественная ось, В₁В₂ – мнимая ось.

Эксцентриситет гиперболы e= >1.

Директрисы гиперболы обладают тем свойством, что отношение расстояния любой точки гиперболы до фокуса к расстоянию до соответствующей директрисы есть величина постоянная, равная эксцентриситету гиперболы.

Уравнение директрис х = или х = .