
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Окружность
Пусть с(а;b) – центр окружности радиуса R, тогда уравнение окружности имеет вид:
(х – а)2 + (y –b)2 = R2 (2)
если сравнить уравнение окружности (2) с общим уравнением кривой 2-го порядка, то нетрудно заметить, что для уравнения окружности выполняются условия: коэффициенты при квадратах неизвестных равны между собой, а член с произведением координат отсутствует, то есть a11=a22, a12=0.
2. Эллипс(в декартовой системе координат)
Эллипсом называется множество точек плоскости, сумма расстояний от которых до двух данный точек, называемых фокусами эллипса, постоянна и равна 2а.
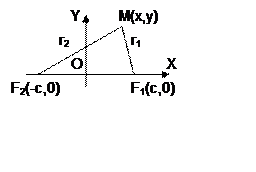 Пусть фокусами эллипса являются точки F1 и F2, при этом F1 F2 = 2с есть фокальная ось эллипса. М – некоторая точка, принадлежащая эллипсу. По определению эллипса, для любой его точки М, имеем:
Пусть фокусами эллипса являются точки F1 и F2, при этом F1 F2 = 2с есть фокальная ось эллипса. М – некоторая точка, принадлежащая эллипсу. По определению эллипса, для любой его точки М, имеем:
МF1 + MF2 = 2а
Пусть ось OX совпадает с фокальной осью F1 F2 . Начало координат выберем посередине между F1 и F2., а ось OY перпендикулярно фокальной оси. При таком выборе системы координат уравнение эллипса примет вид:
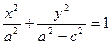 .
.
Так как из ∆ F1МF2 следует , что 2а > 2с т.е. а>с, то полагают а2 – с2 = b2 и получают каноническую (простейшую) форму уравнения эллипса:
 .
.
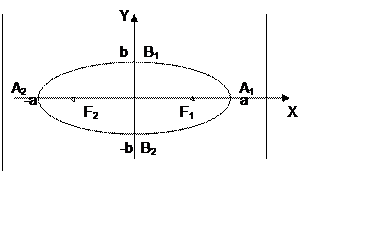 Эксцентриситет эллипса e=
Эксцентриситет эллипса e=  <1.
<1.
|
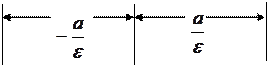
 А1, А2, В1, В2 – вершины эллипса, a директрисы имеют уравнения x=
А1, А2, В1, В2 – вершины эллипса, a директрисы имеют уравнения x=  .
.
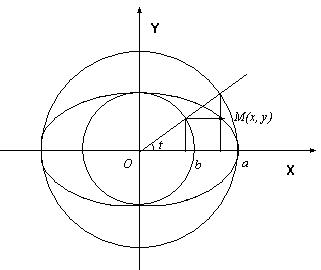
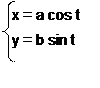 Параметрические уравнения эллипса
Параметрические уравнения эллипса
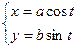
Дата добавления: 2015-04-15; просмотров: 266; Мы поможем в написании вашей работы!; Нарушение авторских прав |