Прямая и плоскость.

1) Угол между прямой и плоскостью.

Углом между прямой и плоскостью называется угол между прямой и ее проекцией на плоскость.

Пусть даны плоскость (a) : Ax+By+Cz+D=0 c нормальным вектором {A,B,C} и прямая

с направляющим вектором 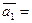{m,n,p}.

Угол между векторами и отличается от угла между прямой и плоскостью на ;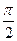

Cos( )= , или sinj= .

2) Условие параллельности прямой и плоскости:

Am+Bn+Cp=0.

3) Условие перпендикулярности прямой и плоскости:

.

Условие того, что прямая лежит в данной плоскости.

Пусть Ax+By+Cz+D=0 данная плоскость (a),

(1) -параметрические уравнения прямой, проходящей через точку М₀(x₀,y_0, z₀), параллельно вектору {m,n,p}.

Условие принадлежности прямой (1) плоскости (a) имеет вид:

.

Если прямая лежит в плоскости, то она этой плоскости параллельна и любая точка прямой удовлетворяет уравнению плоскости.