Задачи на тему “Прямая на плоскости”.

IДаны точки A(-1 2), B(0 –2), C(2 4).

Найти:1) уравнение прямой AB

2) уравнение прямой L₁, проходящей через точку С, параллельно прямой AB;

3) уравнение прямой L₂, проходящей через точку С, перпендикулярно прямой AB;

4) уравнение медианы AD треугольника ABC;

5) уравнение высоты BH;

6) длину высоты BH.

1) На прямой АВ произвольным образом возьмем текущую точку М(x,y) и соединим ее с какой-нибудь известной точкой на этой прямой, например точкой А. Составим текущий вектор {x+1 y-2}.

Вектор 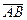{1 -4} расположен параллельно текущему вектору . Следовательно, из условия параллельности, соответствующие координаты этих двух векторов должны быть пропорциональны. Таким образом, получаем уравнение прямой АВ:

, или 4x+y+2=0.

2) На прямой L₁ образуем текущий вектор {x-2 y-4}.

Так как II 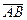, 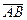{1 -4}, то в силу условия параллельности векторов, получим уравнение прямой L₁:

; или 4x+y-12=0.

3) На прямой L₂ образуем текущий вектор {x-2 y-4}.

Так как 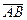, 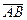{1 -4}, то в силу условия перпендикулярности двух векторов, 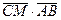=0, получим уравнение прямой L₂:

1(x-2)-4(y-4)=0, или x-4y+14=0.

4) На медиане AD образуем текущий вектор {x+1 y-2}.

Найдем координаты точки D- середины стороны ВС:

X_D= =1, Y_D= =1, D=(1 1).

Образуем вектор {2 -1}, расположенный параллельно текущему вектору . Тогда, в силу условия параллельности векторов, получим уравнение медианы AD:

, или x+2y-3=0.

5) На высоте ВН возьмем текущую точку М(x y) и образуем текущий вектор {x-0 y+2}.

Так как , где {3 2}, то условие перпендикулярности этих векторов порождает уравнение прямой ВН:

3(x-0)+(y+2)=0, или 3x+2y+4=0.

6) Заметим, что длина высоты ВН равна расстоянию от точки В до прямой АС. Чтобы воспользоваться соответствующей формулой расстояния, сначала найдем уравнение прямой АС:

На стороне АС образуем текущий вектор {x+1 y-2}.

Так как II , где {3 2}, то уравнение стороны АС:

, или в общем виде 2x-3y+8=0.

Теперь, подставляя известные данные в формулу расстояния от точки до прямой, имеем:

d= .

Дана прямая L₁: x-2y-3=0 и точка А(-1 2).

Найти:

1) для прямой L₁ уравнение с угловым коэффициентом, угловой коэффициент k, отрезок, отсекаемый по оси ординат;

2) нормаль и направляющий вектор прямой L₁;

3) каноническое уравнение прямой L₁;

4) уравнение прямой L₂, параллельной L₁ и проходящей через точку А;

5) уравнение прямой L₂, перпендикулярной L₁ и проходящей через точку А;

1) Разрешив уравнение прямой относительно Y , получаем уравнение с угловым коэффициентом:

L₁: y=0,5x-1,5. Отсюда k=0,5, b=-1,5.

2) Коэффициенты при переменных X,Y, в общем уравнении прямой L₁, есть координаты нормального вектора, то есть {1 -2}.

Поскольку направляющий вектор {l m} прямой L₁. –это любой ненулевой вектор, параллельный этой прямой, то выполняется условие:

=0, где l²+m² 0.

Дадим величине m какое-нибудь значение. Пусть, например, m =1, тогда

l -2=0, то есть l =2. Получаем направляющий вектор {2 1}.

3) Для составления канонического уравнения прямой L₁ нам необходимо знать точку М₀, лежащую на L₁, и направляющий вектор . Так как координаты вектора ={2 1} были получены нами ранее в задаче 2), осталось найти координаты точки М₀.

Зафиксируем произвольное значение, например, y=0 и подставим его в уравнение прямой L₁. Получим x=3. Следовательно, М₀(3 0). Воспользовавшись теперь каноническим уравнением прямой, находим:

.

4) Прежде всего заметим, что точка А не лежит на прямой L₁, поскольку ее координаты не удовлетворяют уравнению этой прямой. Поэтому можно построить прямую L₂, проходящую через А параллельно L₁, но не совпадающую с L₁:

Пусть М(x y)- текущая точка прямой L₂. Так как текущий вектор {x+1 y-2} перпендикулярен вектору нормали {1 -2} прямой L₁, то =0. Отсюда получаем уравнение прямой L₂:

1(x+1)-2(y-2)=0 или x - 2y + 5 =0

5) Пусть {x+1 y-2}- текущий вектор прямой L₃. Из условия параллельности и нормали {1 -2} прямой L₁, получаем уравнение L₃:

.

III Проверить, являются ли прямые

L₁: 2x+y-4=0, L₂: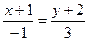

a) параллельными;

b) перпендикулярными;

c) найти угол между L₁ и L₂.

a) Прямые L₁ и L₂ будут параллельны, если их нормали II ₂. Из общего уравнения прямой L₁ найдем координаты нормали {2 1}. Чтобы найти нормаль ₂ приведем уравнение прямой L₂ к общему виду: 3x+y+5=0. Отсюда ₂={3 1}.

Поскольку условие параллельности векторов и ₂ не выполняется, так как , стало быть, L₁ и L₂ непараллельны.

b) Прямые L₁ и L₂ будут перпендикулярны, если ₂. Но условие перпендикулярности для векторов и ₂ не выполняется, так как =7 0. Следовательно, L₁ не перпендикулярна L₂.

d) Угол между прямыми равен углу между их нормалями. Поэтому, используя формулу угла между двумя векторами, получим

cos =соs( , ₂)= .

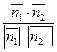Так как =7, , , то cos = .

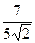Замечания: 1. Если две прямые L₁ и L₂ заданы в каноническом виде, то угол между ними можно рассматривать как угол между их направляющими векторами 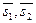, а значит,

cos =соs( , )= .

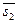2. Если прямые заданы уравнением с угловым коэффициентом, то угол между ними можно вычислить по формуле (1).