Типы уравнений прямой.

Название уравнения определяется названием постоянных величин, определяющих положение прямой в системе координат.

1) Уравнение прямой, проходящей через данную точку М₀(x₀, y₀), перпендикулярно данному вектору {A,B}:

A(x-x₀)+B(y-y₀)=0 (1)

2) Общее уравнение прямой

Ax+By+C=0 (2),

где коэффициенты при неизвестных А, В суть координаты нормального вектора прямой.

Теорема.Всякая прямая на плоскости имеет уравнение первой степени, и всякое уравнение первой степени является уравнением некоторой прямой.

Следствие. a) x=a –уравнение прямой, параллельной оси OY (x=0, уравнение оси OY),

b) y=b- уравнение прямой, параллельной OX (y=0, уравнение OX),

c) y=kx- прямая, проходящая через начало координат. При переменном “k” уравнения пучка прямых, проходящих через начало координат.

3) Уравнение прямой, проходящей через данную точку М₀(x_{0 ,}y₀), параллельно данному вектору {m,n}.

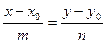(3)

4) Уравнение прямой, проходящей через данную точку в заданном направлении:

y-y₀=k(x-x₀) (4)

Замечание. При переменном k уравнение (4) называется уравнением пучка прямых, проходящих через точку М₀(x₀, y₀).

5) Уравнение прямой с угловым коэффициентом: y=kx+b (5)

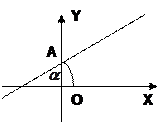Здесь . К виду (5) нельзя привести прямую, параллельную оси ОУ.

6) Уравнение прямой, проходящей через две данные точки:

Замечание. Если x₁=x_0, то уравнение прямой x=x₁; если y₁=y₀ , то y=y_0.