Смешанные задачи на прямую и плоскость.

1)Найти уравнение плоскости, проходящей через точку А(1 –2 3) параллельно прямым

L₁: и L₂: .

На искомой плоскости образуем текущий вектор {x-1 y+2 z-3}. Из канонического уравнения прямой L₁ и параметрического уравнения прямой L₂ получим координаты их направляющих векторов {3 4 -1} и {1 –3 0}. Так как II L_1, II L₂ и L₁IIα, L₂IIα, то IIα, IIα. Поскольку с векторами в пространстве можно совершать параллельный перенос, то можно считать, что α, α.

Так как не параллелен , и для любой точки М(x y z) три вектора , , лежат в плоскости α, то условие ( , , )=0 дает уравнение плоскости α:

.

2)Найти уравнение плоскости, проходящей через точку А(-2 1 0) и прямую L:

.

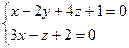На искомой плоскости образуем текущий вектор {x+2 y-1 z}.

Уравнение прямой задано пересечением плоскостей, поэтому ее направляющий вектор определяется из равенств:

= =2 +13 +6 , {2 13 6 }.

Так как II L, L , то .

На прямой L зафиксируем произвольную точку В. Координаты В найдем из системы уравнений заданной прямой, положив в них, например, X=0:

.

Решая эту систему, получим Y=4,5 ,Z=2. Таким образом, В(0; 4,5 ;2). Соединив точки А и В, получим вектор {2; 3,5 ;2}, принадлежащий плоскости α.

Для любой точки М(x y z) выполняется условие компланарности векторов ( , , )=0 и так как

не параллелен , то уравнение плоскости дается равенством:

3)Найти уравнение плоскости α, проходящей через прямые

L₁: и L₂: .

Из канонического уравнения прямой L₁ найдем координаты некоторой точки А, расположенной на L₁: А(1 0 -2) и, соединив ее с текущей точкой М(x y z), образуем текущий вектор {x-1 y z+2} .

Из уравнений прямых получим направляющие вектора {3 2 -1}, {1 –2 3}, которые, как и прямые L₁, L₂, принадлежат плоскости . Так как для любой точки М(x y z) выполняется условие компланарности векторов ( , , )=0, а не параллелен ₂, то искомая плоскость описывается уравнением:

4)Найти уравнение плоскости α, проходящей через прямые

L₁: 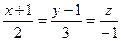и L₂: .

На искомой плоскости возьмем текущую точку М(x y z) и соединим ее с некоторой точкой А(-1 1 0) прямой L₁, координаты которой содержатся в каноническом уравнении этой прямой. Образуем текущий вектор {x+1 y-1 z} . Из уравнений прямых получим направляющие вектора { 2 3 -1}, {-4 –6 2 }, которые принадлежат плоскости . Заметим, что II , значит в составлении уравнения искомой плоскости может участвовать только один из этих векторов, например, . Отсюда возникает необходимость в том, чтобы найти еще один вектор, принадлежащий плоскости и не параллельный . Для этого на прямой L₂ возьмем некоторую точку В. Координаты этой точки получим из уравнения прямой L₂, имеем В(1 0 -3). Составим вектор {2 –1 -3} α.

Для любой точки М(x y z) условие ( , , ) =0 дает уравнение искомой плоскости α:

5)Найти уравнение плоскости α, проходящей через точку А(2 –1 0), перпендикулярно прямой L:

.

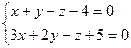На искомой плоскости составим текущий вектор {x-2 y+1 z}.

Найдем направляющий вектор :

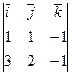= = -2 - , {1-2 -1}.

Для любой точки М(x y z) вектора и перпендикулярны, следовательно, для них выполняется условие ( × )=0, которое дает уравнение плоскости α.: (x-2)-2(y+1)-z=0.

6)Найти уравнение прямой L, проходящей через точку А(1 –3 2 ), перпендикулярно плоскости α :4x-y+2z+3=0.

На прямой L образуем текущий вектор {x-1 y+3 z-2}.

Из общего уравнения плоскости α получим координаты ее вектора нормали {4 –1 2}.

Так как для любой точки М(x y z) L вектора II , то условие коллинеарности

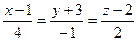
представляет собой уравнение искомой прямой.

7)Найти уравнение плоскости α, проходящей через прямую

L: перпендикулярно плоскости β: 2x-3y+z-1=0.

На плоскости α произвольным образом отметим точку М(x y z). Каноническое уравнение прямой L содержит координаты некоторой точки А(0 1 -2), лежащей на этой прямой. Соединив точки А и М, образуем текущий вектор {x y-1 z+2}. .

Из уравнения прямой L найдем направляющий вектор {2 1 -3}. Так как L , L II , то . Из общего уравнения плоскости β найдем координаты вектора нормали {2 –3 1 }.Поскольку β , β α, то .

Для любой точки М(x y z) вектора , , компланарны. Так как не параллелен , то условие ( , , )=0 порождает уравнение плоскости:

8)Дана прямая L₂: и плоскость α: x-4y+2z+3=0.

a) Проверить, являются ли L и α параллельными.

b) Проверить, являются ли L и α перпендикулярными.

c) Найти угол φ между L и α.

a) Из заданных уравнений получим координаты направляющего вектора {-1 5 3} прямой L и вектора нормали {1 – 4 2 } плоскости.

Если , то L II α. В нашем случае условие перпендикулярности векторов не выполняется, так как ּ =-15 0. Стало быть, L не параллельна α.

b) Если II , то L . В нашем случае условие параллельности векторов не выполняется, так как

. Следовательно, L не перпендикулярна α.

d) Угол между прямой и плоскостью вычислим по формуле:

sin =sin( , )= .

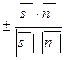Отсюда sin = .

9)Найти точку пересечения прямой и плоскости 2x+3y+3z-9=0.

Параметрическое уравнение прямой имеет вид:

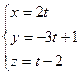. Подставим эти значения X, Y, Z в уравнение плоскости:

4t+3(-3t+1)+3(t-2)-9=0, получим t=-6. Откуда X=-12, Y=19, Z=-8. Следовательно, точка пересечения имеет координаты (-12 19 -8).