Задачи на тему “Прямая в пространстве”.

1)Составить каноническое уравнение прямой L, проходящей через две заданные точки А(1 –2 1), В(3 1 -1).

2) На прямой L возьмем произвольным образом точку М(x y z) и соединим ее с какой-либо известной точкой на этой прямой, например, точкой А. Образуем текущий вектор {x-1 y+2 z-1}. Вектор {2 3 -2}, лежащий на прямой L, является направляющим вектором для L.
Для любой точки М(x y z) L вектора II , следовательно, условие параллельности векторов описывает уравнение прямой L:

.

3)Составить уравнение прямой , проходящей через точку А(1 –1 2), параллельно прямой :

На прямой образуем текущий вектор {x-1 y+1 z-2}. Из канонического уравнения прямой находим направляющий вектор {5 –2 0}, здесь m=5, n=-2, p=0. Так как II , то II для любой точки М(x y z) . Используя теперь условие параллельности, получаем канонические уравнения прямой :

.

4)Известны уравнения двух прямых:

: , :

a) Проверить, являются ли и параллельными.

b) Проверить, являются ли и перпендикулярными.

c) Найти угол между и .

а) Из условия параллельности прямых имеем, II , если их направляющие вектора и параллельны. Координаты вектора легко получаются из заданных канонических уравнений прямой : {-1 3 1}. Для прямой , определяемой пересечением плоскостей, направляющий вектор находится как векторное произведение: = 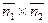, где {1 –1 0}, {2 1 -5}. Вычисляем,

= =5 +5 +3 , {5 5 3}.

Так как координаты векторов и не пропорциональны, то условие параллельности для векторов и не выполняется, а значит, не параллельна .

b) Из условия перпендикулярности прямых, , если . Так как =13, то условие перпендикулярности векторов и не выполняется. Стало быть, не перпендикулярна к .

c) Угол между прямыми найдем по формуле:

cos =соs( , )= .

Отсюда, соs = .

5)Привести к каноническому виду уравнения прямой:

.

Найдем направляющий вектор прямой :

= =-8 -7 -5 , {-8 –7 -5}.

За точку М₀(x₀ y₀ z_o), через которую проходит искомая прямая, можно принять точку пересечения ее с любой из координатных плоскостей, например с плоскостью YOZ. Так как при этом x₀=0, то координаты y_0,z₀ определяются из заданного уравнения прямой, если в нем положить x=0:

.

Откуда находим z₀= , y₀= и M₀(0 ).

Итак, воспользовавшись теперь общей формулой канонических уравнений прямой, получаем:

.