
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задачи на тему “Матрицы”.
1)Найти матрицу С=3Аt-2В, где
А=  , B=
, B=  .
.
 1. Найдем транспонированную матрицу Аt. Для этого в матрице А поменяем местами строки и столбцы:
1. Найдем транспонированную матрицу Аt. Для этого в матрице А поменяем местами строки и столбцы:
Аt=  .
.
2. Все элементы матрицы Аt умножим на 3, а элементы матрицы В на 2, получим:
3At=  , 2B=
, 2B=  .
.
3. Матрица С есть результат вычитания от элементов матрицы 3Аt соответствующих элементов матрицы 2В:
C= 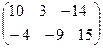 .
. 
2)Найти произведение матриц АВ:
1. A=  , B=
, B=  ;
;
2. A=  , B=
, B=  ;
;
3. A=  , B=
, B=  ;
;
4. A= 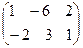 , B=
, B=  .
.
 Заметим, что во всех случаях рассматриваемой задачи, для матриц АВ выполнено условие согласования, то есть, количество столбцов матрицы А совпадает с количеством строк матрицы В, следовательно, АВ определена.
Заметим, что во всех случаях рассматриваемой задачи, для матриц АВ выполнено условие согласования, то есть, количество столбцов матрицы А совпадает с количеством строк матрицы В, следовательно, АВ определена.
1. Так как А(2  3), В(3
3), В(3  2), то АВ(2
2), то АВ(2  2) и
2) и
АВ= 
 =
=  = =
= =  .
.
2. Так как А(2  3), В(3
3), В(3  1), то АВ(2
1), то АВ(2  1) и
1) и
АВ= 
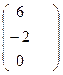 =
=  =
=  .
.
3. Так как А(1  3), В(3
3), В(3  2), то АВ(1
2), то АВ(1  2) и
2) и
АВ= 
 =
=  =(15 11).
=(15 11).
4. Так как А(2  3), В(3
3), В(3  3), то АВ(2
3), то АВ(2  3) и
3) и
АВ= 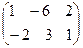
 .=
.=  =
=  .
. 
3)Найти А3, если А= 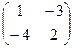 .
.
 Возведение в третью степень матрицы А означает умножение ее трижды на саму себя, то есть А3=ААА.
Возведение в третью степень матрицы А означает умножение ее трижды на саму себя, то есть А3=ААА.
Вначале найдем А2:
AA= 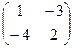
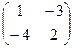 =
=  .
.
Теперь А3=А2А= 
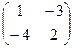 =
=  .
. 
4)Найти АВС, если
А=  , B=
, B=  , C=
, C=  .
.
 В силу свойства ассоциативности матриц: АВС=(АВ)С=А(ВС).
В силу свойства ассоциативности матриц: АВС=(АВ)С=А(ВС).
Выбор последовательности умножения матриц зависит от простоты вычислений. Так, если вначале умножать матрицу А(4  3) на В(3
3) на В(3  2), то образуется матрица АВ размера (4
2), то образуется матрица АВ размера (4  2), а если перемножать В (3
2), а если перемножать В (3  2) и С(2
2) и С(2  1), то получится матрица ВС размера (3
1), то получится матрица ВС размера (3  1) и содержащая меньше искомых элементов, чем АВ.
1) и содержащая меньше искомых элементов, чем АВ.
Находим ВС:
BC= 
 =
=  .
.
Теперь АВС=А(ВС)=
= 
 =
=  .
. 
5)Дана матрица А:
A=  .
.
Найти обратную матрицу  .
.
 Вычислим определитель матрицы А, разложив его по второй строке:
Вычислим определитель матрицы А, разложив его по второй строке:
det(A)=  =-3
=-3  -2
-2  =-4.
=-4.
Так как det(A)¹0, то по теореме об обратной матрице,  определена.
определена.
Найдем алгебраические дополнения соответствующих элементов определителя det(A):
A11= 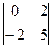 =4 =4
| A21=-  =-8 =-8
| A31=  =4 =4
|
A12=-  =-7 =-7
| A22=  =9 =9
| A32=-  =-5 =-5
|
A13=  =-6 =-6
| A23=-  =10 =10
| A33=  =-6 =-6
|
Строим союзную матрицу  :
:
 =
=  .
.
Следовательно,  =
= 
 =
=  .
. 
6)Найти ранг и базисные миноры матрицы А:
1. A=  ,
,
2. A=  .
.
 1. Вычеркнув из матрицы А нулевые второй, третий столбец и вторую строку, получим матрицу, эквивалентную заданной:
1. Вычеркнув из матрицы А нулевые второй, третий столбец и вторую строку, получим матрицу, эквивалентную заданной:
A~ 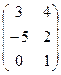 . Так как
. Так как  =26¹0, то ранг исходной матрицы равен 2.
=26¹0, то ранг исходной матрицы равен 2.
Базисными минорами исходной матрицы являются миноры второго порядка, отличные от нуля:
 ,
,  ,
,  .
.
2. Производя последовательно элементарные преобразования, будем иметь:
A~C3+C2  ~C1-C3
~C1-C3  ~
~ 
 .
.
Вычеркнем нулевые первую строку и второй столбец и продолжим преобразования:
A~  ~C2-5C1
~C2-5C1 
 .
.
Ранг последней матрицы равен 2, так как, например,  =3¹0.
=3¹0.
Следовательно, ранг исходной матрицы равен 2, а базисные миноры имеют второй порядок:
 ,
,  ,
,  ,
, 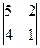 ,
, 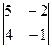 ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 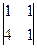 ,
,  ,
,  ,
,  ,
,  .
. 
7)Выяснить, является ли система арифметических векторов линейно зависимой или линейно независимой.
1.  {-3 1 5 2},
{-3 1 5 2},  {-6 2 10 4},
{-6 2 10 4},
2.  {2 –3 1},
{2 –3 1},  {3 –1 5},
{3 –1 5},  {1 –4 3},
{1 –4 3},
3. {0 1 1 -1},  {1 2 0 1},
{1 2 0 1},  {2 3 –1 3},
{2 3 –1 3},  {-1 0 2 –3}.
{-1 0 2 –3}.
 1. Замечаем, что
1. Замечаем, что  =2
=2  . Отсюда имеем, что линейная комбинация l1
. Отсюда имеем, что линейная комбинация l1  +l2
+l2  =0, если l1=2, l2=-1. Следовательно, вектора
=0, если l1=2, l2=-1. Следовательно, вектора  и
и  линейно зависимы по определению.
линейно зависимы по определению.
Случаи 2. и 3. не являются тривиальными, и для их изучения будем использовать критерий линейной зависимости (независимости) векторов: Система векторов линейно зависима (независима) тогда и только тогда, когда ранг матрицы А, составленной из элементов данной системы векторов, меньше (соответственно равен) числа векторов системы.
2. Составим матрицу А, элементарными преобразованиями приведем ее к ступенчатому виду и подсчитаем ранг:
A=  ~C2+C1
~C2+C1  ~C3+C2
~C3+C2  ~C1+2C2
~C1+2C2  ~C1«C2
~C1«C2 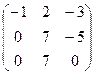 ~
~ 
 .
.
Ранг матрицы А равен трем, поскольку минор  =35
=35  0. Число векторов системы совпадает с рангом, следовательно, исходная система линейно независима.
0. Число векторов системы совпадает с рангом, следовательно, исходная система линейно независима.
3. Аналогично предыдущему, составим и преобразуем матрицу А:
A=  ~C1-C4 , C3-C2
~C1-C4 , C3-C2  ~C2-C1, C4+C1
~C2-C1, C4+C1  ~ ~C3+C2
~ ~C3+C2  ~C4-0,5C2
~C4-0,5C2  ~C3+2C4
~C3+2C4 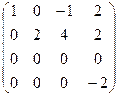 ~ ~
~ ~  ~
~  .
.
Ранг матрицы А равен 3, так как, например, минор
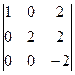 =-4¹0.
=-4¹0.
Число векторов системы равно 4 и не совпадает с рангом, следовательно, исходная система линейно зависима. 
Дата добавления: 2015-04-15; просмотров: 331; Мы поможем в написании вашей работы!; Нарушение авторских прав |