Обратная матрица. Пусть матрица А – квадратная, порядка n

Пусть матрица А – квадратная, порядка n. Левой обратной матрицей по отношению к матрице А называется матрица 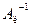того же порядка n, удовлетворяющего равенству

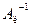А = Е.

Аналогично определяется правая обратная матрица 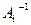, удовлетворяющая равенству: А 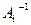=Е.

Если левая и правая обратные матрицы совпадают , то это есть обратная матрица:

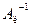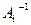= =А^-1

Условием существования обратной матрицы для данной квадратной матрицы является условие d(А)≠0, т.е. матрица не особая. Если матрица А имеет обратную, то эта матрица единственная.

Как найти обратную матрицу:

1.Пусть дана матрица и d(А)≠0.

2.Союзная матрица 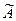- это транспонированная матрица алгебраических дополнений элементов данной матрицы. Элементу а_iк соответствует алгебраическое дополнение А_iк, тогда

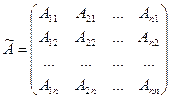и обратная матрица .

Известно, что сумма произведений элементов некоторого ряда на их алгебраические дополнения равна определителю, а сумма произведений элементов некоторого ряда на алгебраические дополнения соответствующих элементов другого ряда равна нулю, поэтому

А^-1 А= 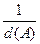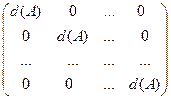= =E.