Лекция 6. Системы линейных алгебраических уравнений.

Однородные системы линейных уравнений.

Матрица А, составленная из коэффициентов при неизвестных

называется матрицей системы.

Числа, стоящие в правых частях уравнений, образуют столбец 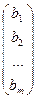, называемый столбцом свободных членов.

Матрица системы, дополненная справа столбцом свободных членов, называется расширенной матрицей системы

В= .

Если свободные члены всех уравнений равны нулю, то система называется однородной.

Определение.Совокупность n чисел х₁⁰,х₂⁰,…х_n⁰ называется решением системы (1), если каждое уравнение системы обращается в числовое равенство после подстановки в него чисел (х₁⁰,х₂⁰,…х_n⁰) вместо соответствующих неизвестных (х₁,х₂,…х_n ).

Системы, не имеющие решений, называются несовместными, а имеющие решения – совместными.

Методы решения системы линейных алгебраических уравнений.