Каноническому виду”.

Пример 1.Найти собственные числа и собственные вектора матрицы

А= .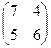

Решение. 1. Решим характеристическое уравнение IА-lЕI=0. В нашем случае оно имеет вид:

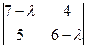=0, то есть l²-13l+22=0.

Собственными числами являются корни характеристического уравнения l₁=2, l₂=11.

2. Собственный вектор ₁, соответствующий числу l₁=2, является базисом в пространстве решений однородной системы

.

Эта система состоит из двух одинаковых уравнений, где неизвестные x₁, x₂ связаны зависимостью

5x₁+4x₂=0, или x₁= 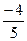x₂.

Положив параметрическую неизвестную x₂ равную произвольной константе, например 1, получим x₁= 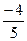и собственный вектор ₁= .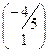

3. Для собственного вектора ₂, соответствующую l₂=11, составим систему

.

Решая ее, придем к соотношению x₁-x₂=0, или x₁=x₂.

Положив x₂=1, получим ₂= .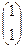

Пример 2. Привести уравнение кривой 5х₁² + 8х₁х₂ + 5х₂² – 18х₁ – 18х₂ + 9 = 0 к каноническому виду. Решение. Составляем определитель δ = 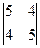=25-16=9>0. Следовательно, кривая эллиптического типа.

1) Матрица группы старших членов А = .

2) Характеристическое уравнение: IА-lЕI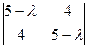=0, =0.

Отсюда ( 5-λ)² – 16 = 0 λ₁=9; λ₂=1.

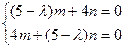
при l₁=9 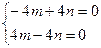, следовательно, при m=n 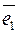{1;1}, I I= , ,

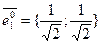при l₂=1 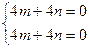, следовательно, при m= - n 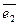{-1;1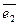}, I I= , ,

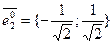3) Матрица перехода к новому базису В = .

4) Преобразование координат при переходе к новому базису

=B ’ или = ,

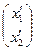формулы преобразования поворота осей координат (перехода к новому базису):

.

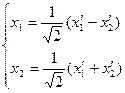5) В новом базисе уравнение линии

,

,

,

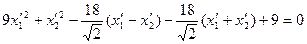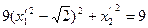6) В новой системе координат центр в точке О₁( 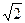; 0), полуоси а=1, b=3.

7) Cтроим график кривой.