Замечание. Пара (Е, (·, ·.)) называется n-мерным Евклидовым пространством; пара (Е,Ф) со свойствами 1)-3) называется n-мерным аффинным пространством.

Определение 8.n-мерным арифметическим Евклидовым пространством называется тройка

:=(Rⁿ, Ф, (·, ·)), где Ф:={A=(x₁,…,x_n): x₁,…,x_n ÎR},"x={x₁,…,x_n}, y={y₁,…,y_n}ÎRⁿ, (x,y):=x₁y₁+…+x_ny_n.

Если А=(x₁,…x_n), B=(y_1,…,y_n), то ={y₁-x₁,…,y_n-x_n}ÎRⁿ.

Определение 8.В n-мерном Евклидовом пространстве совокупность какой-либо точки О (начало координат) и какого-либо базиса ℓ₁… ℓ_n Є Е называется декартовой системой координат (ДСК).

Определение 9. Символом Кронекера называется отображение d_{i, j} : N² ®R, определяемое по правилу:

d_{i, j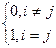}= , i, jÎN.

Определение 10.Базис ℓ₁… ℓ_n в 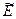называется ортонормированным , если " i, j £ n, (e_{i ,} e_j)= d_{i, j}, то есть элементы его попарно “перпендикулярны ” для i¹j Þ(e_i , e_j)=0, и их нормаль равна 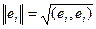1: =1

Определение 11. ДСК, в которой выделенный базис является ортонормированным, называется прямоугольной (ПДСК).

Пример 6.В В₃ со скалярным произведением тройка попарно перпендикулярных векторов 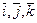единичной длины : 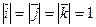, есть пример ортонормированного базиса.

Пример 7.В векторы e₁={1,0,…,0},…,e_n={0,0,…,0,1} образуют ортонормированный базис.

Определение 12. Коэффициенты разложения элемента аÎ Е по базису e_1, e₂,…, e_n : а =a₁e₁+ a₂e₂+…+a_ne_n называются координатами (компонентами) элемента а в базисе e_1, e₂,…, e_n.

Используемая литература

1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 2002.

2. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. – Ростов н/Д: Феникс, 1997.

3. Клетеник Д.В. Сборник задач по аналитической геометрии. – М.: Наука, 1995.

ОГЛАВЛЕНИЕ

Аналитическая геометрия. 3

Лекция 1. Линейные образы в R₂. 3

Задачи на тему “Прямая на плоскости”. 7

Лекция 2. Линейные образы в R₃ . 10

Смешанные задачи на прямую и плоскость. 18

Лекция 3. Кривые второго порядка. 23

Примеры на тему: ”Кривые второго порядка”. 30

Лекция 4. Поверхности второго порядка. 34

Лекция 5. Линейная алгебра. 38

Задачи на тему “Матрицы”. 43

Лекция 6. Системы линейных алгебраических уравнений. 49

Задачи на тему “Системы линейных алгебраических уравнений”. 57

Лекция 7. Понятие линейного преобразования. Собственные векторы. 64

Задачи на темы ”Собственные векторы ”, “Приведение кривой к

каноническому виду”. 68

Лекция 8. Линейные пространства.. 71