Векторы. Вектор- направленный прямолинейный отрезок, т.е

Вектор- направленный прямолинейный отрезок, т.е. отрезок, имеющий определенную длину и определенное направление. Если начало вектора, а его конец, то вектор обозначается символом или . Длиной или модулем вектора называется длина отрезка и обозначается Вектор, длина которого равна нулю, называется нулевым вектором и обозначается Нулевой вектор направления не имеет. Вектор, длина которого равна единице, называется единичным вектором. Векторы и называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают êê . Два вектора и называются равными, если они одинаково направлены и имеют одинаковые длины. Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

Пусть в пространстве задана прямоугольная декартова система координат Выделим в пространстве единичные векторы (орты), обозначаемые , имеющие такие же направления как и координатные оси 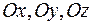соответственно. Любой вектор можно представить в виде линейной комбинации векторов : . В этом случае говорят, что вектор имеет координаты в базисе . Если известны координаты точек и , то координаты вектора равны разностям соответствующих координат его конца и начала: Длину вектора можно найти по формуле

(1.1)

Если векторы , то и при любом действительном .

Пример1.Найти длину вектора , если

Решение. Длину вектора найдем по формуле (1.1)