
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнение прямой с угловым коэффициентом. Положение всякой прямой однозначно определяется любой точкой , лежащей на этой прямой и углом , который образует эта прямая с положительным направлением
Положение всякой прямой однозначно определяется любой точкой  , лежащей на этой прямой и углом
, лежащей на этой прямой и углом 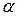 , который образует эта прямая с положительным направлением оси
, который образует эта прямая с положительным направлением оси  . Тангенс угла
. Тангенс угла 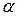 (часто говорят: «угол наклона прямой к оси
(часто говорят: «угол наклона прямой к оси  ») называют угловым коэффициентом прямой. Обозначим:
») называют угловым коэффициентом прямой. Обозначим:  .
.
 |
Заметим, что для прямой, параллельной оси
 , угловой коэффициент
, угловой коэффициент 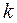 равен нулю, а для прямой, перпендикулярной оси
равен нулю, а для прямой, перпендикулярной оси  , угловой коэффици
, угловой коэффици
Рис. 7
ент не существует. Нетрудно показать, что если прямая не перпендикулярна оси  и имеет направляющий вектор
и имеет направляющий вектор  , то угловой коэффициент
, то угловой коэффициент  .
.
Для того чтобы вывести уравнение прямой, проходящей через заданную точку  и имеющей заданный угловой коэффициент
и имеющей заданный угловой коэффициент 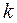 , умножим обе части канонического уравнения (2.4) на
, умножим обе части канонического уравнения (2.4) на  и учтём, что
и учтём, что  . Мы получим искомое уравнение в виде
. Мы получим искомое уравнение в виде 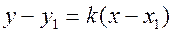 . Если теперь ввести обозначение
. Если теперь ввести обозначение  , то это уравнение примет вид
, то это уравнение примет вид
 . (2.7)
. (2.7)
Оно называется уравнением прямой с угловым коэффициентом.
Пример 23.Написать уравнение прямой, проходящей через точку  и составляющей с осью
и составляющей с осью  угол
угол  .
.
Решение. Найдем угловой коэффициент прямой  Далее подставляя в уравнение
Далее подставляя в уравнение 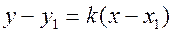
 получим
получим  или
или 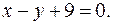
Дата добавления: 2015-04-15; просмотров: 282; Мы поможем в написании вашей работы!; Нарушение авторских прав |