
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнение прямой в отрезках на осях

Рис. 4
Пусть на координатных осях заданы две точки, отличные от начала координат  на оси
на оси 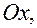
 на оси
на оси  Тогда уравнение прямой, проходящей через эти точки можно записать в виде
Тогда уравнение прямой, проходящей через эти точки можно записать в виде
 (2.3)
(2.3)
где  отрезки, отсекаемые прямой соответственно на осях
отрезки, отсекаемые прямой соответственно на осях  и
и  .
.
Пример 20.Написать уравнение прямой, отсекающей на осях отрезки длиной 2 и 3 соответственно.
Решение. Применим уравнение (2.3). В нашем случае 
 . Преобразуем уравнение к общему виду, для этого умножим обе части уравнения на 6. Имеем
. Преобразуем уравнение к общему виду, для этого умножим обе части уравнения на 6. Имеем 
2.4 Уравнение прямой, проходящей через данную точку  параллельно вектору
параллельно вектору 

Рис. 5
Даны точка  и вектор
и вектор  Требуется написать уравнение прямой
Требуется написать уравнение прямой  , проходящей через точку
, проходящей через точку  параллельно вектору
параллельно вектору  . Пусть
. Пусть  Если
Если  или
или  то
то  или
или 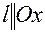 и ее уравнение соответственно имеет вид
и ее уравнение соответственно имеет вид  или
или  Очевидно, что точка
Очевидно, что точка  что имеет место тогда и только тогда, когда координаты
что имеет место тогда и только тогда, когда координаты  пропорциональны соответственным координатам
пропорциональны соответственным координатам  , т.е. когда
, т.е. когда
 . (2.4)
. (2.4)
Это уравнение называют каноническим уравнением прямой, а вектор 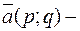 направляющим вектором этой прямой.
направляющим вектором этой прямой.
Пример 21.Написать уравнение прямой, проходящей через точку  параллельно направляющему вектору
параллельно направляющему вектору 
Решение. Воспользуемся уравнением (2.4). Имеем в данном случае 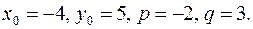 Каноническое уравнение прямой
Каноническое уравнение прямой

 . Приводя подобные члены, получаем общее уравнение прямой
. Приводя подобные члены, получаем общее уравнение прямой 
2.5 Уравнение прямой, проходящей через две заданные точки 

Рис. 6
Точка  принадлежит прямой
принадлежит прямой  тогда и только тогда, когда векторы
тогда и только тогда, когда векторы  и
и  коллинеарны. Следовательно, уравнение прямой, проходящей через две точки, имеет вид
коллинеарны. Следовательно, уравнение прямой, проходящей через две точки, имеет вид
 (2.5)
(2.5)
Пример 22.Написать уравнение прямой, проходящей через точки  и
и 
Решение. Применим уравнение (2.5). Будем считать 
 Подставляем их в уравнение, получим
Подставляем их в уравнение, получим  Упрощая, приходим к общему уравнению прямой
Упрощая, приходим к общему уравнению прямой 
Дата добавления: 2015-04-15; просмотров: 335; Мы поможем в написании вашей работы!; Нарушение авторских прав |