Скалярное произведение и его свойства

Скалярным произведением двух ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла между ними. Обозначается Итак, по определению

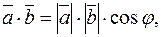где (1.2)

Если хотя бы один из векторов или равен , то скалярное произведение полагается равным 0.

Свойства:

1) переместительный закон.

2) 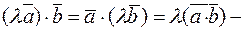сочетательное свойство относительно скалярного множителя

3) распределительный закон.

4)

5) Для того чтобы ненулевые векторы и были взаимно перпендикулярны, необходимо и достаточно, чтобы их скалярное произведение было равно нулю.

6) Если векторы и заданы координатами: то

(1.3)

Из формулы (1.2) найдем

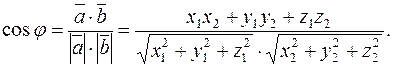(1.4)

Пример 2.Найти скалярное произведение векторов если

Решение. Воспользовавшись свойствами скалярного произведения 1-4 и формулой (1.2), получим

Пример 3.Найти скалярное произведение векторов если

Решение. Найдем координаты векторов и . Вычислим

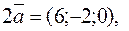тогда

тогда

Воспользовавшись формулой (1.3), получим

Пример 4.Найти косинус угла между векторами и если

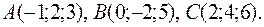
Решение. Найдем координаты векторов и :

Применяя формулу (1.4), получим

=

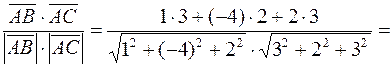
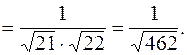
Пример 5.Перпендикулярны ли векторы и

Решение. Вычислим скалярное произведение ненулевых векторов .

следовательно, векторы и перпендикулярны (в силу свойства 5).