Общее уравнение плоскости. в котором , называется общим уравнением плоскости.

Уравнение

(3.1)

в котором 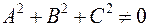, называется общим уравнением плоскости.

3.2 Уравнение плоскости, проходящей через данную точку перпендикулярно .

Пусть в пространстве плоскость задана точкой и вектором ,перпендикулярным этой плоскости. Выведем уравнение плоскости . Возьмем на ней произвольную точку и составим вектор

Рис. 9

Вектор , поэтому , т.е.

(3.2)

Вектор называется нормальным вектором плоскости, а уравнение (3.2) называется уравнением плоскости по точке и нормальному вектору.

Пример 27.Написать уравнение плоскости, проходящей через точку 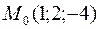перпендикулярно вектору нормали

Решение. Воспользуемся уравнением (3.1). В нашей задаче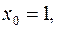

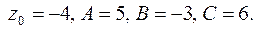
Имеем . Раскрывая скобки и приводя подобные члены получаем общее уравнение прямой