Смешанное произведение векторов. Определение. Смешанным произведением трех векторов , , называется число, равное скалярному произведению вектора

Определение. Смешанным произведением трех векторов , , называется число, равное скалярному произведению вектора на векторное произведение векторов и , т.е. .

Геометрический смысл смешанного произведения выражает следующая теорема.

Теорема. Смешанное произведение равно объему параллелепипеда, построенного на приведенных к общему началу векторах , , , взятому со знаком «плюс», если тройка векторов , , правая, и со знаком «минус», если тройка векторов , , левая. Если же векторы , , компланарны, то .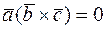

В краткой записи:

Доказательство видно из рисунка.

Свойства смешанного произведения

1. .

2. Величина векторного произведения не изменяется при циклической перестановке сомножителей:

3. векторы компланарны.

4. Смешанное произведение линейно по каждому из сомножителей. В частности,

.

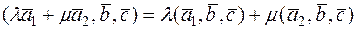Выражение смешанного произведения через координаты сомножителей

Теорема. Если векторы заданы своими координатами: , , , то смешанное произведение равняется определителю, строки которого соответственно равны координатам перемножаемых векторов, т.е.

. (1.6)

Пример 12.Компланарны ли векторы

Решение. Вычислим смешанное произведение векторов по формуле (1.6) , следовательно, векторы - компланарны.

Пример 13.Образуют ли векторы 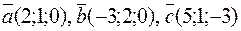базис в пространстве

Проверим, компланарны ли векторы . Для этого вычислим их смешанное произведение

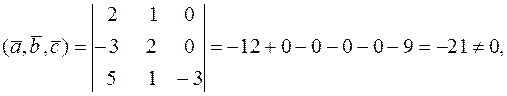следовательно, векторы некомпланарны, а значит, образуют базис в пространстве

Пример 14.Векторы образуют правую тройку, взаимно перпендикулярны и Вычислить

Решение.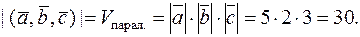

Пример 15.Найти объем параллелепипеда, построенного на векторах

Решение.

Пример 16.Найти объем тетраэдра с вершинами в точках

Решение. Найдем координаты векторов

Вычислим объем параллелепипеда, построенного на векторах

Пример 17.Лежат ли точкив одной плоскости?

Решение. Найдем координаты векторов

Проверим, компланарны ли векторы

, для этого вычислим их смешанное произведение:

следовательно, векторы некомпланарны, а, значит, точки не лежат в одной плоскости.