КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Векторное произведение векторов. Результатом перемножения двух векторов может быть не только скаляр, но и вектор
Результатом перемножения двух векторов может быть не только скаляр, но и вектор. Понятие векторного произведения, о котором пойдет речь в этом пункте, является объектом изучения теории трехмерного евклидова пространства. В евклидовом пространстве, число измерений которого отлично от трех, не имеется аналогий этого понятия.
Тройка векторов называется упорядоченной, если указано, какой из них считается первым, какой – вторым и какой – третьим. При записи тройки векторов мы всегда будем располагать эти векторы в порядке их следования (если для нас будет небезразличен порядок набора). Так, запись 
, 
, 
означает, что первым элементом тройки является вектор , вторым – вектор и третьим – вектор .
Упорядоченная тройка некомпланарных[1] векторов , , называется правой, если, находясь внутри трехгранного угла, образованного приведенными к общему началу векторами , , , мы видим кратчайший поворот от к и от него к совершающимся против часовой стрелки. В противном случае тройка называется левой.
Удобное практическое правило определения правой тройки: упорядоченная тройка некомпланарных векторов , , является правой, если после приведения к общему началу векторы располагаются так, как могут быть расположены соответственно большой, указательный и средний пальцы правой руки.
Определение. Векторным произведением вектора на вектор называется вектор , обозначаемый символом 
(или 
) и удовлетворяющий следующим трем требованиям:
1) длина вектора равна 
, где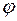 
– угол между векторами и , т.е. площади параллелограмма, построенного на векторах и , как на сторонах;
2) вектор ортогонален плоскости векторов и ( 
, 
);
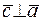3) векторы , , образуют правую тройку векторов.
Требования 1 и 2 определяют вектор с точностью до двух взаимно противоположных направлений; требование 3 отбирает одно из этих двух направлений. В случае, когда и коллинеарные, тройка , , является компланарной, но в этом случае уже из требования 1 следует, что 
.
 |
Понятие векторного произведения (так же, как и скалярное произведение[2]) родилось в механике. Если вектор
изображает приложенную в некоторой точке 
силу, а вектор идет из некоторой точки 
в точку , то вектор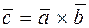 
представляет собой момент силы относительно точки .
Свойства векторного произведения
1. 
векторы и – коллинеарны. В частности 
.
2. 
(антикоммутативность).
3. 
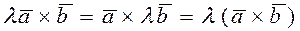, для любого 
(однородность).
4. 
,
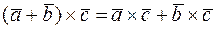(дистрибутивность).
Если векторы , заданы своими координатами в базисе 
, т.е. 
то
(1.5)
Пример 6.Найти векторное произведение векторов 
и 
Решение. Воспользуемся формулой (1.5)
Пример 7. Найти площадь параллелограмма, построенного на векторах
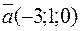и 
Решение. Найдем площадь параллелограмма, построенного на векторах
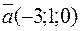и 
, как длину их векторного произведения, т.е.
. Сначала найдем
.
Пример 8. Найти площадь параллелограмма, построенного на векторах 
и 
, если 
Решение. Согласно 1-му пункту определения векторного произведения имеем: = 
Пример 9.Найтиплощадь треугольника, построенного на векторах 
если 
Решение.
При вычислении воспользовались свойствами векторного произведения 1-4, т.е. 
Пример 10.Найти площадь треугольника с вершинами в точках 
Решение. 
составляет половину площади параллелограмма, построенного на векторах 
и 
, как на сторонах. Найдем координаты векторов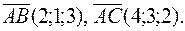 
Вычислим 
:
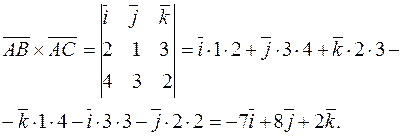
Пример 11.Найти 
, если 
,
Решение. Найдем координаты векторов 
и 
Вычислим 
Найдем длину векторного произведения:
Дата добавления: 2015-04-15; просмотров: 83; Мы поможем в написании вашей работы!; Нарушение авторских прав |