Гипербола. Определение. Гиперболой называется геометрическое место точек плоскости, для которых абсолютная величина разности расстояний до двух фиксированных точек и

Определение. Гиперболой называется геометрическое место точек плоскости, для которых абсолютная величина разности расстояний до двух фиксированных точек и , называемых фокусами, есть величина постоянная.

Каноническое уравнение гиперболы (5.2)

Рис.13

Гипербола, заданная уравнением (5.2), симметрична относительно осей координат (рис. 13). Она пересекает ось 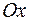в точках 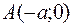и − вершинах гиперболы и не пересекает ось . Параметр 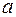называется вещественной полуосью, мнимой полуосью. Параметр есть расстояние о фокуса до центра. Отношение называется эксцентриситетом гиперболы.

Эксцентриситет для гиперболы

Прямые называются асимптотами гиперболы.

Пример 38. Построить гиперболу 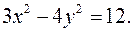Найти 1) действительную и мнимую полуоси; 2) координаты фокусов; 3) эксцентриситет; 4) уравнения асимптот.

Решение. 1) Запишем уравнение гиперболы в канонической форме Действительная полуось гиперболы 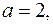мнимая полуось 2) Найдем Фокусы гиперболы 3) Эксцентриситет найдем по формуле 4) Уравнения асимптот Построим гиперболу.

Рис. 14