ЛИНЕЙНАЯ АЛГЕБРА

ЛИНЕЙНАЯ АЛГЕБРА

ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ

АЛГЕБРА МАТРИЦ. ДЕЙСТВИЯ НАД МАТРИЦАМИ

ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ МАТРИЦ

ОПРЕДЕЛИТЕЛИ

СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ

НЕВЫРОЖДЕННЫЕ МАТРИЦЫ

РАНГ МАТРИЦЫ

СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ. ТЕОРЕМА КРОНИКЕРА-КАПЕЛЛИ

РЕШЕНИЯ НЕВЫРОЖДЕННЫХ ЛИНЕЙНЫХ СИСТЕМ ФОРМУЛОЙ КРАМЕРА

РЕШЕНИЕ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ ГАУССА

СИСТЕМА ЛИНЕЙНЫХ ОДНОРОДНЫХ УРАВНЕНИЙ

ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ

ПРОЕКЦИЯ ВЕКТОРА НА ОСЬ

ОСНОВНЫЕ СВОЙСТВА ПРОЕКЦИЙ

РАЗЛОЖЕНИЕ ВЕКТОРА ПО ОРТАМ КООРДИНАТНЫХ ОСЕЙ

РАВЕНСТВО ВЕКТОРОВ

КОЛЛИНЕАРНОСТЬ ВЕКТОРОВ

КООРДИНАТЫ ВЕКТОРА

КООРДИНАТЫ ТОЧКИ

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

ВЫРАЖЕНИЕ СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ ЧЕРЕЗ КООРДИНАТЫ

НЕКОТОРЫЕ ПРИЛОЖЕНИЯ СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ

ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

ВЫРАЖЕНИЕ ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ ЧЕРЕЗ КООРДИНАТЫ СОМНОЖИТЕЛЕЙ

НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ

26. СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ТРЁХ ВЕКТОРОВ

СВОЙСТВА СМЕШАННОГО ПРОИЗВЕДЕНИЯ ВЕКТОРОВ

ВЫРАЖЕНИЕ СМЕШАННОГО ПРОИЗВЕДЕНИЯ ЧЕРЕЗ КООРДИНАТЫ

НЕКОТОРЫЕ ПРИЛОЖЕНИЯ СМЕШАННОГО ПРОИЗВЕДЕНИЯ

30. РЕШЕНИЯ ЗАДАЧ ПО ТЕМЕ: «ВЕКТОРНАЯ АЛГЕБРА».

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ

РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ НА ПЛОСКОСТИ

ПЛОЩАДЬ ТРЕУГОЛЬНИКА

ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС ОСЕЙ КООРДИНАТ

ПОВОРОТ ОСЕЙ КООРДИНАТ

ЛИНИИ НА ПЛОСКОСТИ (ОСНОВНЫЕ ПОНЯТИЯ)

УРАВНЕНИЯ ПРЯМОЙ НА ПЛОСКОСТИ

ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ. ОСНОВНЫЕ ЗАДАЧИ

ВОПРОСЫ К ЭКЗАМЕНУ

ЛИНЕЙНАЯ АЛГЕБРА

Тема: ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ

Матрицей, называется прямоугольная таблица чисел, содержащая m-строк одинаковой длины или n-столбцов одинаковой длины. Матрицу записывают в виде:

или

где

Матрицу А, называют матрицей размера m*n.

Числа а_ij, составляющие матрицу, называются ее элементами. Элементы, стоящие по диагонали идущей из верхнего левого угла, образуют главную диагональ.

Матрицы равны между собой, если равны все соответствующие элементы этих матриц.

Матрица, у которой число строк равно числу столбцов, называется квадратной.

Квадратную матрицу размера n*n, называют матрицей n-го порядка.

Квадратная матрица, у которой все элементы, кроме элементов главной диагонали равны нулю, называется диагональной.

Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной матрицей и обозначается Е.

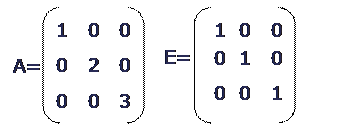
Квадратная матрица, называется треугольной, если все элементы, расположены по одну сторону от главной диагонали равной нулю.

Матрица все элементы, которой равны нулю, называется нулевой, обозначается буквой О. в матричном исчислении, матрицы О и Е играют роль 0 и 1 в арифметике.

Матрица, содержащая один столбец или одну строку, называется вектором.

Матрица, размера 1*1, состоящая из 1-го числа, отождествляется с этим числом.

7_1*1=7

Матрица, полученная из данной, заменой ее строки, столбцом с тем же номером, называется матрицей транспортированной к этой матрице. Обозначается в виде:

А^Т

Транспортированная матрица обладает следующим свойством:

(А^Т)^Т=А

Для операции транспортирования верны следующие ему свойства:

1) (А+В)^Т=А^Т+В^Т

2) (АВ)^Т=А^ТВ^Т

Тема: АЛГЕБРА МАТРИЦ. ДЕЙСТВИЯ НАД МАТРИЦАМИ

Сложение.Операция сложения матриц вводится только для матриц одинакового размера.

А_m*n=(a_ij)

B_m*n=(b_ij)

Суммой двух матриц А и В, называется матрица С_m*n=(c_ij), такая, что

c_ij= a_ij+b_ij,

C=А+В

Аналогично определяется разность матриц

Произведение.Произведение матрицы А_m*n=(a_ij) на число к, называется матрица B_m*n=(b_ij), такая что b_ij=к* a_ij

В =к*А

Произведение матриц.Операция умножения матриц вводится только для случая, когда число столбцов одной матрицы равны числу строк второй матрицы. Произведение матрицы А_m*n=(a_ij) на матрицу В_n*р =(b_jk), называется матрица С_m*р =(с_ik), такая, что с_ik=a_i1* b_1k+ a_i2* b_2k+…+ a_in * b_nk

Т.е. элемент i-строки и к-столбца, матрица произведение С равной сумме произведений элементов i-строки матрицы А на соответствующие элементы к-столбца матрицы В.

Получение элемента с_ik схематически изображается

Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют. Легко доказать, что если А*Е=Е*А=А, где А – квадратная матрица, а Е – единичная матрица того же размера. Матрицы А и В, называются перестановочными, если АВ=ВА. Умножение матриц обладает следующими свойствами, если конечно написанные суммы и произведения матриц имеют смысл.

Свойства:

1) А(ВС)=(АВ)С

2) А(В+С)=АВ+АС

3) (А+В)С=АС+ВС

4) α(АВ)=(αА)В

Матрица –А=(-1)*А, называется противоположной матрице А. В разность матрицу А-В можно определить, как А+(-В).

Операция сложения и умножения матриц на число обладают следующими свойствами:

1) А+В=В+А

2) А+(В+С)=(А+В)+С

3) А+0=А

4) А-А=0

5) 1*А=А

6) α(А+В)=αА+αВ

7) (α+β)А=αА+βА

8) α(βА)=(αβ)А

где А, В и С – матрицы, а α и β – числа.

Тема: ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ МАТРИЦ

Элементарными преобразованиями матриц являются:

1. перестановка местами двух параллельных рядов матрицы

2. умножение всех элементов ряда матрицы на число отличное от нуля

3. прибавление ко всем элементам ряда матрицы в соответствие элементов параллельного ряда умноженных на одно и тоже число

Две матрицы А и В, называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований А~В. При помощи элементарных преобразований любую матрицу можно привести к матрице, из которой в начале главной диагонали стоит подряд несколько единиц, а все остальные элементы равны нулю, такую матрицу, называют канонической.

Тема: ОПРЕДЕЛИТЕЛИ

Квадратная матрица А порядка n можно сопоставить число det A или |А|, Δ от латинского слова determine – определяют, называется определителем. Определитель вычисляют следующим образом:

1. при n=1, определитель матрицы А=(а_n)

det A=|а_n|

2. при n=2, то матрица

3. при n=3, для матрицы

Правило треугольника – Саррюса, который вкратце отображается

Тема: СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ

Свойства:

1. равноправность строк и столбцов

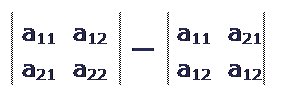
Определитель не изменится, если его строки заменить столбцами и наоборот. В дальнейшем строки и столбцы определителя будет просто, называться рядами определителя.

2. при перестановки двух параллельных рядов определитель меняет знак

3. определитель, имеющий два одинаковых ряда равен нулю

4. общий множитель элементов, какого-либо ряда определителя можно вывести за знак определителя

Из свойств 3 и 4 следует, что если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен нулю.

5. если элементы, какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей

6. элементарное преобразование определителя, определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда умножив на любое число

Минором, некоторого элемента a_ij определителя n-го порядка, называется определитель n-1 порядка, полученный из исходного путем вычеркивания строки и столбца на пересечении, которых находится выбранный элемент. Обозначается m_ij.

Алгебраическим дополнением элемента a_ij определителя, называется его минор, взятый со знаком плюс, если сумма i+j – четное число и со знаком минус, если эта сумма нечетная.

А_ij=(-1)^i+jm_ij

7. разложение определителя по элементам некоторого ряда

Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения (свойство 7 содержит в себе способ вычисления определителей высоких порядков).

8. сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения, соответствующих элементов параллельного ряда равно нулю

а₁₁*А₂₁+а₁₂*А₂₂+а₁₃*А₂₃=0

Тема: НЕВЫРОЖДЕННЫЕ МАТРИЦЫ

Пусть А квадратная матрица n-го порядка

Квадратная матрица А, называется невырожденной, если ее определитель не равен нулю (Δ=det А≠0), если определитель равен нулю (Δ=0), то матрица вырождена.

Матрицей союзной к матрице А, называется такая матрица,

где А_ij – алгебраическое дополнение к данной матрице элемента а_ij. Оно определяется также, как и алгебраическое дополнение элемента определителя.

Матрица А^-1, называется обратной к матрице А, если выполняется условие А* А^-1=Е, при чем А^-1*А=Е, где Е – единичная матрица того же порядка, что и матрица А, А^-1 – обратная матрица, имеет те же размеры, что и матрица А.

Теорема:

Всякая невырожденная матрица имеет обратную

т.е.

Свойства обратной матрицы:

1)

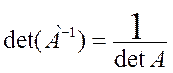
2) (АВ)^-1=В^-1А^-1

3) (А^-1)^Т=(А^Т)^-1

Тема: РАНГ МАТРИЦЫ

Рассмотрим матрицу А размером m*n

Выделим в ней к-строк и к-столбцов. Таким образом, чтобы к ≤ min (m, n) из элементов, стоящих на пересечении, выделенных строк и столбцов составим определитель к-го порядка. Все такие определители, называются минорами этой матрицы, заметим, что таких миноров можно составить такое число:

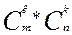, где число сочетаний из n элементов по к. наибольший из порядков миноров данной матрицы отличных от нуля, называется рангом матрицы и обозначается:

R (A) = rang A

Очевидно, что 0 ≤ r ≤ min (m, n). Минор к-го порядка определяющий ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров.

Найти ранг матрицы А.

Все миноры 3-го порядка равны нулю, есть минор 2-го порядка отличный от нуля.

Базисный минор стоит на пересечении 2 и 3 строки с 1 и 3 столбцами.

Свойства ранга:

1. при транспонировании матрицы ее ранг не меняется

2. если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не меняется

3. ранг матрицы не изменяется при элементарных преобразованиях матрицы

Ранг канонической матрицы равен числу единиц на главной диагонали. На этом основан один из способов вычисления ранга матрицы.

r (A) = 2

Тема: СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

Системой линейных алгебраических уравнений, содержащей m уравнений и n неизвестных, называется система вида:

где числа а_ij

, называются коэффициентами системы, а b_i – свободными членами, подлежат нахождению числа х_n. Такую систему удобно записывать в компактной матричной форме: (*) А*х=В, где А – матрица коэффициентов системы.

, называется основной матрицей.

х – это вектор столбец из неизвестных х_j

В – вектор столбец из свободных b_i

Произведение матриц АХ определено, т.к. в матрице А столбцов столько же сколько строк в матрице Х, т.е. n штук.

Расширенной матрицей системы, называется матрица Ā дополненная столбцами свободных членов

Решением системы, называется n значений неизвестных х₁=С₁, х₂=С₂, … х_n=C_n, при подстановки, которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде матрицы столбца:

.

Система, называется совместной, если она имеет хотя бы одно решение и несовместной, если она не имеет не одного решения. Совместная система, называется определенной, если она имеет единственное решение и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение, называется частным решением системы. Совокупность всех частных решений, называется общим решением. Решить систему это значит выяснить, совместна она или несовместна. Если система совместна – найти ее общее решение. Две системы, называются эквивалентными или равносильными, если они имеют одно и то же общее решение. Другими словами системы эквивалентны, если каждое решение одной из них является решением другой и наоборот.

Эквивалентные системы получаются в частности при элементарных преобразованиях системы. При условии, что преобразования выполняются лишь над строками матрица.

Система линейных уравнений, называется однородной, ели все свободные члены равны нулю. Однородная система всегда совместна, т.к. х₁=х₂=х₃ … х_n=0 является решением системы. Это решение, называется нулевым или тривиальным.

Тема: РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ. ТЕОРЕМА КРОНИКЕРА-КАПЕЛЛИ

Пусть дана произвольная система m линейных уравнений с n неизвестными (см. *).

Исчерпывающий ответ на вопрос о совместности этой системы дает теорема Кроникера-Капелли. Эта теорема будет состоять из 3-х теорем:

1. система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы. Правила практического разыскания всех решений совместной системы линейных уравнений вытекают из следующих теорем

2. если ранг совместной матрицы системы равен силу неизвестных. То система имеет единственное решение

3. если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений

Правила решения произвольной системы линейных уравнений:

1. найти ранг основной и расширенной матрицы системы, если ранг основной матрицы системы не равен рангу расширенной системы, то система несовместна

2. если ранг системы равен рангу расширенной системы и равен рангу (какому-то числу). То система совместна. Найти какой-либо базисный минор порядка к, взять к уравнений из коэффициентов, которых состоит базисный минор. Неизвестное коэффициентов, которых входит в базисный минор, называют главным и оставляют слева, а остальные уравнения, оставшиеся n – ранг неизвестных, называются свободными и переносят в правую часть уравнения

3. найти в выражении главные неизвестных через свободные. Получено общее решение системы

4. придавая свободным неизвестным произвольные значения, получим соответствующие главные неизвестных. Таким образом, можно найти частные решения исходной системы уравнений

Тема: РЕШЕНИЯ НЕВЫРОЖДЕННЫХ ЛИНЕЙНЫХ СИСТЕМ ФОРМУЛОЙ КРАМЕРА

Пусть дана система n линейных уравнений с n неизвестными (см. *).

Основная матрица А, такой системы – квадратная. Определитель этой матрицы

называется определителем системы. Если определитель системы отличен от нуля, то такая система невырождена. Найдем решение системы уравнения, в случае, когда определитель не равен нулю. Умножив обе части уравнения записанного в матричной форме Ах=В, *А^-1 получим А^-1Ах= А^-1В. Поскольку выражения равны Е*(х)=х, то получаем х= А^-1В. Отыскание решения по этой формуле (1), называется матричным способом решения системы.

Матричное равенство 1 записываем в следующем виде:

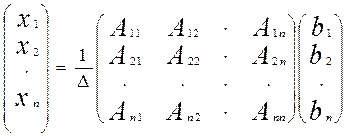т.е.

, но

А₁₁b₁+A₂₁b₂+…+A_1nb_n, есть разложение определителя

Разложение этого определителя по элементам 1-го столбца, т.е. b₁ умноженное на дополнение. Определитель Δ₁, получается путем замены первого столбца с коэффициентом столбцом из свободных членов.

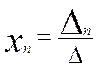- т.к. получено путем замены n-го столбца. Столбцом из свободных членов, формулы

причем 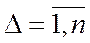, называется формулами Крамера.

И так, невырожденная система n линейных уравнений с n неизвестными имеет единственное решение, которое может быть найдено матричным способом 1 по формуле Крамера 2.

Пример:

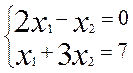
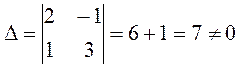
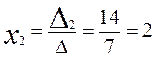
Ответ: х₁=1, х₂=2.

Тема: РЕШЕНИЕ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ ГАУССА

Одним из наиболее универсальных и эффективных методов решений систем алгебраических уравнений является метод Гаусса, состоящий в последовательном исключении неизвестных. Пусть дана система:

Процесс решения по методу Гаусса состоит из двух этапов. На первом этапе, который будет называться, прямой ход – система, приводится к ступенчатому виду, в частностях к треугольному:

, к ≤ n, a_ii ≠ 0,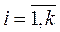

Коэффициент а_ii, называется главным элементом системы. На 2-м этапе, который называется – обратный ход, идет последовательное определение неизвестных из этой ступенчатой системы.

Решим систему методом Гаусса:

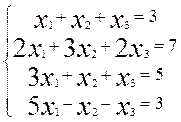
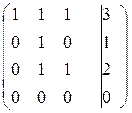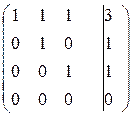~ ~ r=3

х₁+х₂+х₃=3

х₂ =1

х₃=1

х₁+2=3

х₁ =1

Тема: СИСТЕМА ЛИНЕЙНЫХ ОДНОРОДНЫХ УРАВНЕНИЙ

Пусть дана система однородных линейных уравнений:

Система однородных уравнений всегда совместна и она имеет нулевое решение.

Теорема 4:

Для того, чтобы система однородных уравнений имела ненулевое решение необходимо и достаточно, чтобы ее ранг основной матрицы был меньше числа неизвестных (r < n).

Теорема 5:

Для того, чтобы система однородная система с n линейных уравнений с n неизвестными имела ненулевое решение необходимо и достаточно, чтобы ее определитель был равен нулю.

Тема: ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ

Векторы. Основные понятия.

Величины, которые полностью определены своим численным значением, называются скалярными. Другие величины, которые определены не только своим числовым значением, но и направлением, называются векторные. Векторная величина геометрически изображается с помощью вектора.

Вектор – это направленный прямолинейный отрезок, т.е. отрезок имеющий определенную длину и определенное направление. Если Ā начало вектора, а его конец, то вектор обозначается символом или . Вектор , называется противоположным вектору . Вектор, противоположный вектору , обозначается - .

Длиной или модулем вектора , называется длина отрезка и обозначается . Вектор длина, которого равняется нулю, называется нулевым и обозначается, как 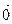(нулевой вектор направления не имеет). Вектор длина, которого равна единице, называется единичным вектором и обозначается 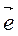. Единичный вектор направление, которого совпадает с вектором , называется ортом вектора и обозначается . Вектора и , называются коллинеарными, если они лежат на одной прямой или на параллельных прямых и обозначается ║ . Коллинеарные вектора могут быть направлены одинаково ↑↑ или противоположно ↓↑ в одну сторону или со направлены в разные стороны. Нулевой вектор считается коллинеарным любому вектору. Два вектора и , называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые длины, т.е. вектора равны, если равны их модули и совпадает направление.

Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора помещать в любую точку О пространств, т.е. свободный вектор.

На рисунке векторы образуют прямоугольник, причем , а вектор (вектора и противоположные).

Три вектора в пространстве, называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трех векторов, хотя бы один нулевой или два любые коллинеарны, то такие вектора компланарны.

Вектора бывают:

1. свободный – это такой вектор, который переносится параллельно самому себе в пространстве. Характеризуется модулем и направлением. Точка начала вектора может быть любая точка в пространстве

2. скользящий – это вектор расположен на линии скольжения или действия. Характеризуется направлением и модулем. Точка начала вектора может быть любая точка на линии принадлежащая линии

3. связанный – это вектор точка начала вектора является фиксированной. Сам вектор характеризуется направлением и модулем.

Угол между векторами, называется наименьшим. Угол между векторами, имеющий общую точку начала

Угол между вектором и осью. Ось – это прямая с выбранным положительным направлением.

Угол между заданным вектором и осью, называется угол между заданным вектором и орт вектором.