Линейные операции над векторами.

Под линейными операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число.

Пусть и два произвольных вектора. Возьмем произвольную точку О и построим вектор . От точки отложим вектор . Вектор соединяет начало первого вектора с концом второго, называющийся суммой векторов и .

Это правило сложения векторов, называется правилом треугольника. Сумму двух векторов можно построить по правилу параллелограмма.

Сложение трех векторов используем

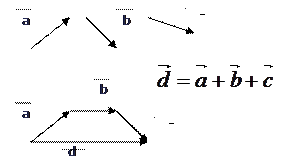
Под разностью векторов и понимается вектор , такой что

Отметим, что в параллелограмме построенном на векторах и одна направленная диагональ является суммой векторов и , а другая разностью.

Можно вычитать по следующему правилу:

, т.е. вычитание векторов заменим – сложить вектор с противоположным вектору .

Произведение вектора на скаляр или число λ, называется вектор λ* или * λ, который имеет длину , коллинеарен вектору имеет направление вектора (λ > 0) и противоположное направление, если λ < 0

Из определения произведения вектора на число, следует свойство этого произведения:

1. если = λ* , то ║ . Наоборот, если и коллинеарны, причем = 0, то при некотором λ верно равенство = λ*

2. каждый вектор равен произведению его модуля на орт = *

Свойство линейных операций над векторами:

1.

2.

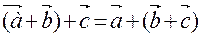
3.

4.

5.

Эти свойства позволяют проводить преобразования в линейных операциях с векторами, т.к. это делается в обычной алгебре, а именно слагаемые менять местами, вводить скобки, группировать и выносить за скобки, как скаляры, так и векторные общие множители.

Тема: ПРОЕКЦИЯ ВЕКТОРА НА ОСЬ

Выражение «проекция вектора 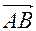на ось ОХ» употребляется в двух разных смыслах: геометрическом и алгебраическом (арифметическом).

1. Проекцией (геометрической) вектора 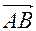на ось ОХ, называется вектор (рис 1) начало, которого А^' есть проекция начала А на ось ОХ, а конец В^' – проекция конца В на ту же ось.

Обозначение: Пр_ОХ 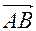или, короче, Пр 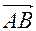. Если ось ОХ задана вектором , то вектор , называется также проекцией вектора 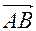на направление вектора и обозначается Пр_с .

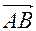Геометрическая проекция вектора на ось ОХ, называется также компонентой вектора по оси ОХ.

2.Проекцией (алгебраической) вектора 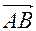на ось ОХ(или на направление вектора ), называется длина вектора , взятая со знаком плюс или минус, смотря по тому, имеет ли вектор то же направление, что и ось ОХ (вектор ), или противоположное.

Обозначение: Пр_ОХ 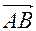или Пр_с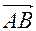

Замечание: геометрическая проекция (компонента) вектора есть вектор, а алгебраическая проекция вектора есть число.

Пример 1. Геометрическая проекция вектора (рис 2) на ось ОХ, есть вектор . Его направление противоположно направлению оси, а длина (при единице масштаба ОЕ) равна 2. значит, алгебраическая проекция вектора на ось ОХ, есть отрицательное число -2.

,

Если векторы 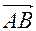и (рис 3) равны, то их алгебраические проекции по одной и той же оси тоже равны . То же для геометрических проекций.

Алгебраические проекции одного и того же вектора на две равнонаправленные оси (О₁Х₁ и О₂Х₂, рис 4) равны (если оси параллельны, но противоположно направлены, то алгебраические проекции не равны, они отличаются знаком) ( ). То же для геометрических проекций.

3. Связь между компонентой (геометрической проекцией) и алгебраической проекцией вектора. Пусть есть вектор, равнонаправленный с осью ОХ и имеющий длину 1. Тогда геометрическая проекция (компонента) какого-либо вектора , по оси ОХ равна произведению вектора на алгебраическую проекцию вектора по той же оси:

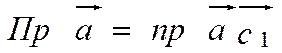
Пример 2. При обозначениях рис 2 имеем

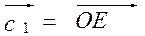. Геометрическая проекция вектора на ось ОХ есть вектор , алгебраическая проекция того же вектора есть число -2 (см пример 1). Имеем:

Тема: ОСНОВНЫЕ СВОЙСТВА ПРОЕКЦИЙ

Если , то

Если ( ), то (см рис 1)

Если , то

Свойство 1. Проекция вектора на ось l равна произведению модуля вектора на cos угла φ медлу вектором и осью, т.е.

Следствие 1.1. Проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол – прямой.

Следствие 1.2. Проекция равных векторов на одну и ту же ось равны между собой.

Пусть, например, 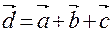, имеем , т.е. 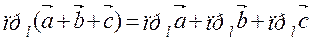(см рис 2)

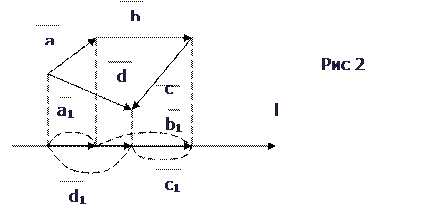
Свойство 2. Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось.

Свойство 3. При умножении вектора на число λ его проекция на ось также умножается на это число, т.е. .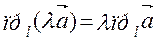

При λ > 0 имеем (свойство 1)

При λ < 0:

Свойство справедливо, очевидно, и при λ = 0.

Таким образом, линейные операции над векторами приводят к соответствующим линейным операциям над проекциями этих векторов.

Тема:РАЗЛОЖЕНИЕ ВЕКТОРА ПО ОРТАМ КООРДИНАТНЫХ ОСЕЙ

Рассмотрим в пространстве прямоугольную систему координат Oxyz. Выделим на координатных осях ОХ, ОУ и OZ единичные векторы (орты), обозначаемые i , j , k соответственно (см. рис. 3).

Рис.3

Выберем произвольный вектор пространства и совместим его начало с началом координат: = .

Найдем проекции вектора на координатной оси. Проведем через конец вектора плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно через , и 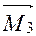. Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор . Тогда , , . По определению суммы нескольких векторов находим .

А так как , , то .

Обозначим проекции вектора = на оси ОХ, ОУ и OZ соответственно через , и , т.е. , , 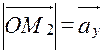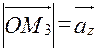. Тогда получаем:

Эта формула является основной в векторном исчислении и называется разложением вектора по ортам координатных осей. Числа , , , называются координатами вектора , т. е. координаты вектора есть его проекции на соответствующие координатные оси.

Векторное равенство часто записывают в символическом виде: .

Равенство означает, что . Зная проекции вектора , можно легко найти выражение для модуля вектора. На основании теоремы о длине диагонали прямоугольного параллелепипеда можно написать , т.е.

т. е. модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат.

Пусть углы вектора с осями ОХ, ОУ и OZ соответственно равны a,b,g. По свойству проекции вектора на ось, имеем , , 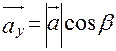. Или, что, то же самое, , , . Числа cos α, cos β, cos γ , называются направляющими косинусами вектора .

Подставим выражения , , 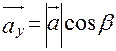в равенство ,получаем:

Сократив на получим соотношение: ,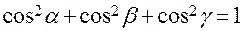

т. е. сумма квадратов направляющих косинусов ненулевого вектора равна единице.

Легко заметить, что координатами единичного вектора 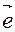являются числа cos α, cos β, cos γ , т.е.

Итак, задав координаты вектора, всегда можно определить его модуль и направление, т.е. сам вектор.