КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Угол между двумя прямыми и условия параллельности перпендикулярности двух прямых
Пусть прямые L1 и L2 заданы уравнениями с угловыми коэффициентами рис. 22
у = к1х + b1 и у = к2х + b2 (см. рис. 22).
Требуется найти угол φ, на который надо повернуть в положительном направлении прямую L1 вокруг точки их пересечения до совпадения с прямой L2.
Решение: Имеем α2 = φ + α1(теорема и внешнем угле треугольника) или φ=α2 -α1. Если φ≠π/2, то
Ho tg α1 = к1, tg α2= k2, поэтому
(2.12)
откуда легко получим величину искомого угла.
Если требуется вычислить острый угол между прямыми, не учитывая, какая прямая является первой, какая — второй, то правая часть формулы (2.12) берется по модулю, т. е
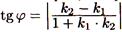
Если прямые L1 и L2 параллельны, то φ = 0 и tg φ = 0. Из формулы (2.12) следует к2 - к1 =0, т. е. к2 = к1. И обратно, если прямые L1 и L2 таковы, что к1=к2, то tg φ = 0, т. е. прямые параллельны.
Следовательно, условием параллельности двух прямых является равенство их угловых коэффициентов: к1=к2
Если прямые L1 и L2 перпендикулярны, то φ = π/2. Следовательно,
Отсюда 1 + к1• к2 = 0, т. е. к1• к2 = -1( или к2 =- 1/к1)
Справедливо и обратное утверждение. Таким образом,условием перпендикулярности прямых является равенство к1• к2 = -1
Расстояние от точки до прямойрис. 23
Пусть заданы прямая L уравнением Ах + By + С = 0 и точка М(хо;уо) (см. рис. 23). Требуется найти расстояние от точки M0 до прямой L.
Решение: Расстояние d от точки Мо до прямой L равно модулю проекции вектора М1Мо, где M1(x1;y1) - произвольная точка прямой L, на направление нормального вектора п = (А;В). Следовательно,
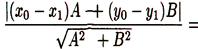
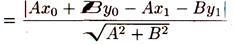
Так как точка M1(x1;y1) принадлежит прямой L, то Ах1 +- Ву1 + С = 0, т. е
С =- Ах1 – Ву1. Поэтому
(2.13)
что и требовалось получить.
ВОПРОСЫ К ЭКЗАМЕНУ ПО ДИСЦИПЛИНЕ: «ВЕКТОРНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ»
1. Элементы линейной алгебры
2. Алгебра матриц. Действия над матрицами
3. Элементарные преобразования матриц
4. Определители. Минор матрицы. Алгебраическое дополнение
5. Свойство определителей
6. Невырожденные матрицы. Обратная матрица. Расширенная матрица
7. Ранг матрицы
8. Системы линейных уравнений (основные понятия)
9. Теорема Кроникера-Капелли
10. Решение систем линейных уравнений (произвольной и невырожденной)
11. Формулы Крамера
12. Метод Гаусса для решения систем линейных уравнений
13. Системы линейных однородных уравнений
14. Элементы векторной алгебры
15. Векторы (основные понятия)
16. Линейные операции над векторами
17. Свойства линейных операций над векторами
18. Проекция вектора на ось
19. Основные свойства проекций
20. Разложение вектора по ортам координатных осей
21. Модуль вектора
22. Действия над векторами, заданными проекциями
23. Равенство векторов
24. Коллинеарность векторов
25. Координаты вектора
26. Координаты точки
27. Скалярное произведение векторов и его свойства
28. Выражение скалярного произведения через координаты
29. Некоторые приложения скалярного произведения
30. Векторное произведение векторов и его свойства
31. Выражение векторного произведения через координаты
32. Некоторые приложения векторного произведения
33. Смешанное произведение векторов
34. Свойства смешанного произведения векторов
35. Выражение смешанного произведения через координаты
36. Некоторые приложения смешанного произведения
37. Декартова система координат на плоскости
38. Полярная система координат на плоскости
39. Расстояние между двумя точками на плоскости
40. Деление отрезка в данном отношении
41. Параллельный перенос осей координат
42. Поворот осей координат
43. Линии на плоскости (основные понятия)
44. Параметрические уравнения на линии
45. Уравнение прямой с угловым коэффициентом
46. Общее уравнение прямой
47. Уравнение прямой, проходящей через точку в данном направлении
48. Уравнение пучка прямых с центром в точке
49. Уравнение прямой, проходящей через две точки
50. Уравнение прямой в отрезках
51. Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору
52. Полярное уравнение прямой
53. Нормальное уравнение прямой
54. Угол между двумя прямыми и условия параллельности и перпендикулярности двух прямых
55. Расстояние от точки до прямой
Дата добавления: 2015-04-15; просмотров: 243; Мы поможем в написании вашей работы!; Нарушение авторских прав |