КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Преобразование системы координат.
Переход от одной системы координат в какую-либо другую называется преобразованием системы координат.
Рассмотрим два случая преобразования одной прямоугольной системы координат в другую. Полученные формулы устанавливают зависимость между координатами произвольной точки плоскости в разных системах координат.
Тема: ПОВОРОТ ОСЕЙ КООРДИНАТ
Под поворотом осей координат понимают такое преобразование координат, при котором обе оси поворачиваются на один и тот же угол, а начало координат и масштаб остаются неизменными.
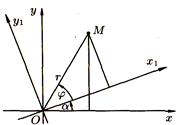Пусть новая система О1х1у1 получена поворотом системы Оху на угол α (см. рис. 6).
Пусть М — произвольная точка плоскости, (х; у) — ее координаты старой системе и (х';у') — в новой системе.
Введем две полярные системы координат с общим полюсом О и полярными осями Ох и Ох1 (масштаб одинаков). Полярный радиус r в обеих системах одинаков, а полярные углы соответственно равны α + φ и φ , где φ — полярный угол в новой полярной системе.
По формулам перехода от полярных координат к прямоугольным имеем
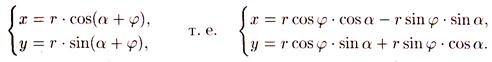
Но r *cos φ = х' и r * sin φ = у'. Поэтому
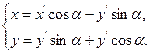
Полученные формулы называются формулами поворота осей.Они позволяют определять старые координаты (х; у) произвольной точки М через новые координаты (х';у') этой же точки М, и наоборот.
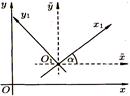
Рис. 7
Если новая система координат О1х1у1 получена из старой Оху путем параллельного переноса осей координат и последующим поворотом осей на угол α (см. рис. 7), то путем введения вспомогательной системы О1х1у1 легко получить формулы, выражающие старые координаты х и у произвольной точки через ее новые координаты х' и у'.
Тема: ЛИНИИ НА ПЛОСКОСТИ (ОСНОВНЫЕ ПОНЯТИЯ)
Линия на плоскости часто задается как множество точек, обладающих некоторым только им присущим геометрическим свойством. Например, окружность радиуса R есть множество всех точек плоскости, удаленных на расстояние R от некоторой фиксированной точки О (центра окружности).
Введение на плоскости системы координат позволяет определять положение точки плоскости заданием двух чисел — ее координат, а положение линии на плоскости определять с помощью уравнения (т. е. равенства, связывающего координаты точек линии).
Уравнением линии (или кривой) на плоскости Оху называется такое уравнение F(x; у) = 0 с двумя переменными, которому удовлетворяют координаты х и у каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.
Переменные х и у в уравнении линии называютсятекущими координатами точек линии.
Уравнение линии позволяет изучение геометрических свойств линии заменить исследованием его уравнения.
Так, для того чтобы установить лежит ли точка А(хо, уо) на данной линии, достаточно проверить (не прибегая к геометрическим построениям), удовлетворяют ли координаты точки А уравнению этой линии в выбранной системе координат.
Задача о нахождении точек пересечения двух линий, заданных уравнениями F1(x;y) = 0 и F2(x;y) = 0, сводится к отысканию точек, координаты которых удовлетворяют уравнениям обеих линий, т. е. сводится к решению системы двух уравнений с двумя неизвестными:
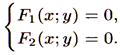
Если эта система не имеет действительных решений, то линии не пересекаются.
Аналогичным образом вводится понятие уравнения линии в полярной системе координат.
Уравнение F(r; φ) =0 называется уравнением данной линии в полярной системе координат, если координаты любой точки, лежащей этой линии, и только они, удовлетворяют этому уравнению.
Линию на плоскости можно задать при помощи двух уравнений:
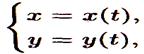(1)
где x и у — координаты произвольной точки М(х;у), лежащей на данной линии, a t — переменная, называемая параметром; параметр t определяет положение точки (х; у) на плоскости.
Например, если х = t + 1, у = t2, то значению параметра t = 2 соответствует на плоскости точка (3; 4), т. к. х= 2 + 1 = 3, у = 22 = 4.
Если параметр t изменяется, то точка на плоскости перемещается, описывая данную линию. Такой способ задания линии называется параметрическим, а уравнения (1) — параметрическими уравнениями линии.
Чтобы перейти от параметрических уравнений линии к уравнению вида F(x;y) = 0, надо каким-либо способом из двух уравнений исключить параметр t. Например, от уравнений
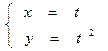
путем подстановки t = х во второе уравнение, легко получить уравнение у = х2; или у — х2 = 0, т. е. вида F(x; у) = 0. Однако, заметим, такой переход не всегдацелесообразен и не всегда возможен.
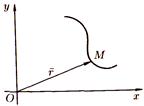Линию на плоскости можно задать векторным уравнением r = r (t), где t — скалярный переменный параметр. Каждому значению toсоответствует определенный вектор r0 = r (t0), плоскости. При изменении параметра t конец вектора r = r (t) опишет некоторую линию (см. рис. 8).
Векторному уравнению линии r = r (t) всистеме координат Оху соответствуют два скалярных уравнения (1), т. е. уравнения проекций на оси координат векторного уравнения линии есть ее параметрические уравнения. рис. 8
Векторное уравнение и параметрические уравнения линии имеют механический смысл. Если точка перемещается на плоскости, то указанные уравнения называются уравнениями движения, а линия — траекторией точки, параметр t при этом есть время.
Итак, всякой линии на плоскости соответствует некоторое уравнение вида F(x;y) = 0.
Всякому уравнению вида F(x;y) = 0 соответствует, вообще говоря, некоторая линия, свойства которой определяются данным уравнением
(выражение «вообще говоря» означает, что сказанное допускает исключения.
Так, уравнению (х - 2)2 + {у - З)2 = 0 соответствует не линия, а точка (2; 3); уравнению х2 + у2 + 5 = 0 на плоскости не соответствует никакой геометрический образ).
В аналитической геометрии на плоскости возникают две основные задачи. Первая: зная геометрические свойства кривой, найти ее уравнение; вторая: зная уравнение кривой, изучить ее форму и свойства.
На рисунках 9-17 приведены примеры некоторых кривых и указаны их уравнения.
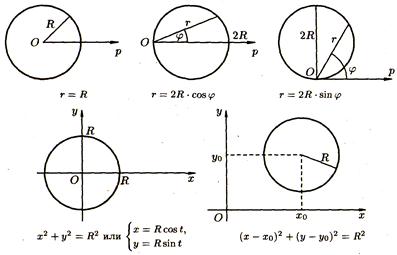
Рис. 9. Окружность радиуса R
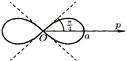
Рис. 10. Лемниската Бернулли
Уравнение в прямоугольных координатах: (х2 + у2)2 - а2(х2 - у2) = 0, а > 0;
в полярных координатах: r = а√cos2φ
Рис. 11. Трехлепестковая роза
В полярных координатах ее уравнение имеет вид r = а cos3φ 3, где а > 0.
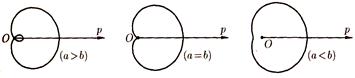
Рис. 12. Улитка Паскаля
Уравнение в полярных координатах имеет вид r = b +а cosφ .
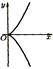
Рис 13. Полукубическая парабола
Уравнение кривой у2 = х3 или
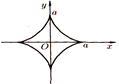
Рис. 14. Астроида
Уравнение в прямоугольных координатах: х2/3+y2/3 =а2/3; параметрические уравнения:
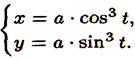
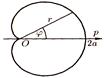
Рис. 15. Кардиоида
Уравнение в полярных координатах мест вид r = а(1+ cosφ), где а > 0. Кардиоида — частный случай улитки Паскаля (а = b).
Рис. 16. Спираль Архимеда
Уравнение кривой в полярных координатах r = а φ ,где а > 0— постоянное.
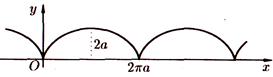
Рис. 17. Циклоида
Параметрические уравнения циклоиды имеют вид
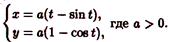
Циклоида — это кривая, которую описывает фиксированная точка окружности, катящаяся без скольжения по неподвижной прямой.
Тема: УРАВНЕНИЯ ПРЯМОЙ НА ПЛОСКОСТИ
Простейшей из линий является прямая. Разным способам задания прямой соответствуют в прямоугольной системе координат разные виды ее уравнений.
Уравнение прямой с угловым коэффициентом
Пусть на плоскости Оху задана произвольная прямая, не параллельная оси Оу. Ее положение вполне определяется ординатой b точки N(0;b) пересечения с осью Оу и углом α между осью Ох и прямой (см. рис. 18).
Под углом α (0≤ α < π) наклона прямой
рис. 18понимается наименьший угол на который нужно повернуть вокруг точки пересечения прямой и оси Оx против часовой стрелки ось Ох до ее совпадения с прямой.
Возьмем на прямой произвольную точку М(х;у) (см. рис. 18). Проведем через точку N ось Nx', параллельную оси Ох и одинаково с ней направленную
Угол между осью Nx'. и прямой равен а. В системе Nx'y точка М имеет координаты х и у-b.
Из определения тангенса угла следует равенство
| tga= | у-b |
| х |
, т. е. у = tga*x + b. Введем обозначение tga = k, получаем уравнение у = кх + b, (2.2)
которому удовлетворяют координаты любой точки М(х;у) прямой
Можно убедиться, что координаты любой точки Р(х;у), лежащей вне данной прямой, уравнению (2.2) не удовлетворяют.
Число к = tgaназывается угловым коэффициентомпрямой, а уравнение (2.2) — уравнением прямой с угловым коэффициентом.
Если прямая проходит через начало координат, то b= 0 и, следовательно, уравнение этой прямой будет иметь вид у = кх.
Если прямая параллельна оси Ох, то a = 0, следовательно, к =tga = 0 и уравнение (2.2) примет вид у = b.Если прямая параллельна оси Оу, то a =π/2, уравнение (2.2) теряет смысл, т. к. для нее угловой коэффициент к = tga = tg π/2 не существует. В этом случае уравнение прямой будет иметь вид
х = а,(2.3)
а- абсцисса точки пересечения прямой с осью Ох. Отметим, что уравнения (2.2) и (2.3) есть уравнения первой степени.
Дата добавления: 2015-04-15; просмотров: 177; Мы поможем в написании вашей работы!; Нарушение авторских прав |