Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору

Найдем уравнение прямой, проходящей через заданную точку М(х_о;у_о) перпендикулярно данному ненулевому вектору п = (А; В). рис.20

Возьмем на прямой произвольную точку М(х;у)и рассмотрим вектор = (х — х_о;у— у_о) (см. рис. 20). Поскольку векторы п и 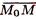перпендикулярны, то их скалярное произведение равно нулю: п* МоМ = 0, то есть

А(х - х₀) + В (у - уо) = 0. (2.8)

Уравнение (2.8) называется уравнением прямой, проходящей через заданную точку перпендикулярно заданному вектору.

Вектор п = (А; В), перпендикулярный прямой, называется нормальным вектором этой прямой.

Уравнение (2.8) можно переписать в виде

Ах + Ву + С = 0, (2.9)

где А и В — координаты нормального вектора, С= Ах_о — Ву₀ — свободный член.

Уравнение (2.9) есть общее уравнение прямой (см 2.4)

Полярное уравнение прямойрис.21

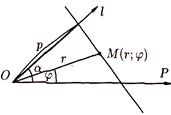
Найдем уравнение прямой в полярных координатах. Ее положение можно определить, указав расстояние р от полюса О до данной прямой и угол α между полярной осью ОР и осью l, проходящей через полюс О перпендикулярно данной прямой (см. рис. 21).

Для любой точки М(r;φ) на данной прямой имеем:

С другой стороны,

Следовательно,

(2.10)

Полученное уравнение (2.10) и есть уравнение прямой в полярных координатах.