Действия над векторами, заданными проекциями.

Пусть векторы и заданы своими проекциями на оси координат OX, OУ, OZ или что то же самое

,

Тема: РАВЕНСТВО ВЕКТОРОВ

Определение.Два (ненулевых) вектора и равны, если они равнонаправлены и имеют один тот же модуль. Все ненулевые векторы считаются равными. Во всех остальных случаях векторы не равны.

Пример 1. Векторы 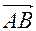и (рис 5) равны.

Пример 2. Векторы и (рис 6) не равны (хотя у них длины и одинаковы), т.к. их направления различны. Векторы и то же не равны, а векторы и равны.

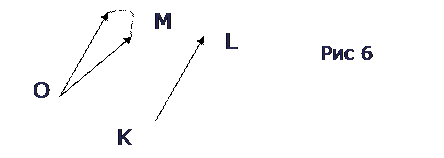
Предостережение.Нельзя смешивать понятие «равенство векторов» с понятием «равенство отрезков». Говоря: «отрезки ON и KL равны», мы утверждаем, что один из них можно совместить с другим. Но для этого может понадобиться поворот совместимого отрезка (как в расположении рис 6). В таком случае согласно определению векторы и не равны. Два вектора будут равны лишь в том случае, когда их можно совместить без поворота.

Обозначения.Запись = , выражает, что векторы и равны. Запись ≠ выражает, что векторы и не равны. Запись = , выражает, что модули (длины) векторов и равны, при этом сами векторы и могут равняться, а могут и не равняться друг другу.

Пример 3. 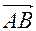= (рис 5), ≠ , = , = (рис 6).

Тема: КОЛЛИНЕАРНОСТЬ ВЕКТОРОВ

Векторы, лежащие на параллельных прямых (или на одной и той же прямой), называются коллинеарными. Векторы , , на рис 7 коллинеарны. Векторы , , на рис 8 коллинеарны.

Коллинеарные векторы могут иметь одно и то же направление (равнонаправленные векторы) или противоположные. Так, векторы и (рис 7) равнонаправлены, векторы и (а также и ) противоположно направлены. Векторы и на рис 8 равнонаправлены, векторы и противоположно направлены.

Тема: КООРДИНАТЫ ВЕКТОРА

Определение. Прямоугольными координатами вектора 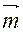, называются алгебраические проекции вектора 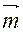на оси координат. Координаты вектора обозначаются большими буквами X, Y, Z (координаты точки маленькими).

Запись: или

Вместо того, чтобы проецировать вектор 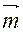на оси OX, OY, OZ можно проецировать его на оси М₁А, М₁В, М₁С (рис 9) проведенные через начало М₁ вектора 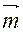и равнонаправленные с осями координат.

Пример 1. Найти координаты вектора 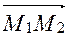(рис 9) относительно системы координат ОХУZ. Через точку М₁ проводим оси М₁А, М₁В, М₁С соответственно равнонаправленные с осями OX, OY, OZ.

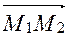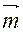Через точку М₂ проводим плоскости М₂Р, М₂Q, М₂R параллельно координатным плоскостям. Плоскости М₂Р, М₂Q, М₂R пересекут оси М₁А, М₁В, М₁С соответственно в точках Р, Q, R. Абсцисса Х вектора есть длина вектора , взятая со знаком минус; ордината У вектора есть длина вектора , взятая со знаком минус; аппликата Z – длина вектора , взятая со знаком плюс. При масштабе рис 9 Х=-4, У=-3, Z=2.

Запись: или

Если два вектора и равны, то координаты соответственно равны:

Координаты вектора не меняются при параллельном переносе системы координат. Напротив, координаты точки при параллельном переносе системы координат меняются.

Если начальная точка О вектора соответственно равны координатам конечной его точки М.

Пример 2. У вектора на рис 10 абсцисса Х=2, ордината У=-3, аппликата Z=2. те же координаты имеет точка М.

Запись: 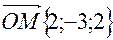или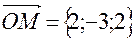

Тема: КООРДИНАТЫ ТОЧКИ

Положение любой точки М в пространстве можно определить тремя координатами следующим образом: через точку М проводим плоскости МР, МQ, МR (рис 10) соответственно параллельно плоскостям XOZ, ZOX, XOY. В пересечении с осями получаем точки Р, Q, R. Числа х (абсцисса), у (ордината), z (аппликата) (латинское слово «аппликата» (applicata) в переводе означает «приложенная» (точку М можно построить так: сначала взять на плоскости XOY точку L с координатами х=ОР, у=РL, а затем «приложить» отрезок МL=z, перпендикулярно плоскости XOY)), измеряющие отрезки ОР, ОQ, ОR в избранном масштабе, называются (прямоугольными) координатами точки М. они берутся положительными или отрицательными, смотря по тому имеют ли векторы соответственно те же направления, что и основные векторы I, j, k или противоположные.

Пример. Координаты точки М на рис 10 есть: абсцисса х=2, ордината у=-3, аппликата z=2.

Запись: М(2;-3;2)

Вектор , идущий от начала координат О к некоторой точке М, называется радиусом-вектором точки М и обозначается буквой r; чтобы отличать друг от друга радиусы-векторы разных точек, при букве r ставят значки: так, радиус-вектор точки М обозначается r_М. радиусы-векторы точки А₁, А₂, … , А_n, обозначается r₁, r₂, … r_n.

Тема: СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

Скалярным произведением двух ненулевых векторов и , называется число равное произведению длин этих векторов на cos угла между ними (1), где . Формуле 1 можно придать иной вид:

, тогда получаем 2-ю формулу: (2), т.е. скалярное произведение двух векторов равно модулю одного из них умноженной на проекцию другого на ось сонаправленную с первым вектором.

Свойства:

1. скалярное произведение обладает переместительным свойством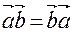

доказательство:

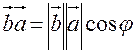
2. скалярное произведение обладает сочетательным свойством относительно скалярного множителя

доказательство: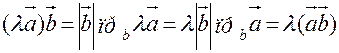

3. скалярное произведение обладает распределительным свойством

доказательство:

4. скалярный квадрат вектора равен квадрату его длины

доказательство:

Если вектор возвести скалярно в квадрат, а затем извлечь корень, то получим не первоначальный вектор, а его модуль

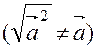
5. если векторы и не нулевые, взаимно перпендикулярны, то их скалярное произведение равно нулю: ┴ , =0, справедливо и обратное утверждение =0, ≠0, ≠0 ┴

доказательство: т.к. угол φ=(а^b)= , то cos φ = cos =0

= 0=0

Если =0, а ≠0 и ≠0, то cos угла равен нулю при 90^○ ┴

Тема: ВЫРАЖЕНИЕ СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ ЧЕРЕЗ КООРДИНАТЫ

Пусть задано два вектора и :

,

Найдем скалярное произведение векторов, перемножая их, как многочлены, что законно в силу свойств линейности скалярного произведения. И пользуясь таблицей скалярности произведения векторов:

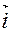
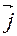
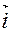
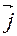
Записываем: ;

и так скалярное произведение векторов равно сумме произведений их одноименных координат.

Тема: НЕКОТОРЫЕ ПРИЛОЖЕНИЯ СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ

1. угол между векторами. Определение угла φ между ненулевыми векторами

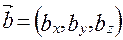
отсюда следует условие перпендикулярности ненулевых векторов и :

┴

2. проекция вектора на заданное направление. Нахождение проекции вектора на направление заданные вектором может осуществляться по формуле:

, ;

,

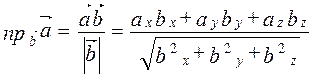3. работа постоянной силы. Пусть материальная точка перемещается прямолинейно из положения А в положение В под действием постоянной силы F, образующий угол φ с перемещением АВ равному какому-то S:

Из физики известно, что работа силы F при перемещении S: , . Таким образом работа постоянной силы при прямолинейном перемещении ее точки приложения равно скалярному произведению вектора силы на вектор перемещения.

Тема: ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

Определение. Упорядоченная тройка некомпланарных векторов называется правой, если из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки.

Векторным произведением вектора 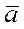на вектор называется вектор такой, что:

1) ,

2) и ,

3) образуют правую тройку векторов.

Понятие векторного произведения также пришло из механики: если – это сила , приложенная в точке М, вектор = , то векторное произведение – это момент силы относительно точки О.

M

O

Свойства векторного произведения: