
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теорема 3.
Пусть векторы  имеют в ортонормированном базисе координаты
имеют в ортонормированном базисе координаты  . Тогда смешанное произведение этих векторов можно представить в виде
. Тогда смешанное произведение этих векторов можно представить в виде
 .
.
доказательство. 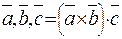 .
.
По теореме о векторном произведении:
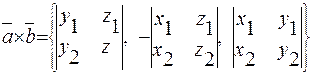 .
.
Умножим векторное произведение скалярно на вектор  :
:
 .
.
По следствию 2 необходимым и достаточным условием компланарности трех векторов является равенство нулю определителя, составленного из координат векторов:
 компланарны.
компланарны.
Пример 3. Даны четыре точки:  . Найти объем тетраэдра АВСD.
. Найти объем тетраэдра АВСD.
Решение. Объем тетраэдра равен одной шестой объема параллелепипеда с теми же основанием и высотой:
 .
.
Координаты векторов  .
.
По теореме 3
 .
.
Тема: НЕКОТОРЫЕ ПРИЛОЖЕНИЯ СМЕШАННОГО ПРОИЗВЕДЕНИЯ
Определение взаимной ориентации векторов в пространстве:
Определение взаимной ориентации векторов а, b и с основано на следующих соображениях. Если abc > 0 , то а , b , с — правая тройка; если abc <0 , то а, b , с - левая тройка.
Установление компланарности векторов:
Векторы а, b и с компланарны тогда и только тогда, когда их смешанное произведение равно нулю 

Определение объемов параллелепипеда и треугольной пирамиды:
Нетрудно показать, что объем параллелепипеда, построенного на векторах а, b и с вычисляется как V =|аbс|, а объем треугольной пирамиды, построенной на этих же векторах, равен V =1/6*|abc |.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ТЕМЕ: «ВЕКТОРНАЯ АЛГЕБРА».
Задача 1. Разложить вектор  по векторам
по векторам 


Решение. Разложить вектор 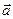 по векторам
по векторам  – значит представить его в виде
– значит представить его в виде
 (1)
(1)
где 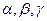 - неизвестные пока числа. Переходя в равенстве (1) к координатам векторов, получим
- неизвестные пока числа. Переходя в равенстве (1) к координатам векторов, получим

Как известно у равных векторов равны соответствующие координаты,
 (2)
(2)
Решив систему (2), найдём 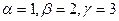 . Следовательно,
. Следовательно,  .
.
Задача 2. Найти вектор  коллинеарный вектору
коллинеарный вектору  и удовлетворяющий условию
и удовлетворяющий условию 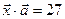 .
.
Решение. В силу коллинеарности векторов 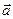 и
и  вектор
вектор  можно представить в виде
можно представить в виде  где
где  – пока неизвестный множитель. Для его определения используем второе условие:
– пока неизвестный множитель. Для его определения используем второе условие:
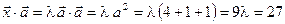 .
.
Отсюда  , поэтому
, поэтому  .
.
Задача 3. Найти вектор  , перпендикулярный векторам
, перпендикулярный векторам 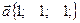 и
и 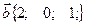 и образующий с осью Ох тупой угол, если
и образующий с осью Ох тупой угол, если 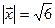 .
.
Решение. Найдём вектор 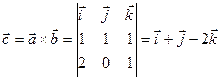 .
.
Так как  перпендикулярен векторам
перпендикулярен векторам 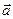 и
и  , то он коллинеарен вектору
, то он коллинеарен вектору  . Следовательно,
. Следовательно, 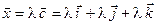 .
.
По условию  т.е.
т.е.  или
или 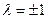 . Вектор
. Вектор  образует тупой угол с осью Ох, поэтому его проекция на эту ось должна быть отрицательной, отсюда
образует тупой угол с осью Ох, поэтому его проекция на эту ось должна быть отрицательной, отсюда  и
и  .
.
Дата добавления: 2015-04-15; просмотров: 241; Мы поможем в написании вашей работы!; Нарушение авторских прав |