Углы Эйлера. Уравнения сферического движения тела.

Рис. 39.

Через неподвижную точку тела O проведем неподвижную прямоугольную декартовую систему координат Ox₁y₁z₁, относительно которой будем рассматривать движение тела (рис. 39). Другую систему координат Oxyz скрепим с телом.

Линия OK пересечения координатных плоскостей Ox₁y₁ и Oxy называется линией узлов.

Для определения положения тела относительно неподвижной системы координат используются углы Эйлера.

Угол j между линией узлов OK и подвижной осью Ox называется углом собственного вращения. При изменении угла j тело вращается вокруг так называемой оси собственного вращения Oz.

Угол y между неподвижной осью и линией узлов называется углом прецессии. Для изменения угла y тело должно вращаться вокруг оси Oz₁, которую называют осью прецессии.

Угол q между осями Oz и Oz₁ называется углом нутации, а ось OK, вокруг которой вращается тело при изменении угла q, называется осью нутации или линией узлов.

Для определения положения тела с одной неподвижной точкой в любой момент времени достаточно задать углы Эйлера, как функции времени:

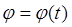, y = y (t), q = q (t). (30)

Эти уравнения являются уравнениями сферического движения тела.