Определение ускорений точек плоской фигуры с помощью МЦУ.

Рис. 33.

Если при определении ускорений точек плоской фигуры полюсом выбрать МЦУ этой фигуры (рис. 33), то, как следует из теоремы 4, ускорение любой точки плоской фигуры равно ускорению за счет вращения фигуры вокруг полюса. А оно в свою очередь равно сумме вращательного ускорения и осестремительного ускорения вокруг оси, перпендикулярной плоскости фигуры и проходящей через МЦУ (точку Q):

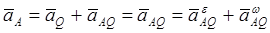
Величина ускорения точки плоской фигуры пропорциональна расстоянию от точки до МЦУ и определяется выражением:

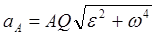. (28)

Вектор ускорения точки плоской фигуры 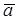_A лежит в плоскости фигуры и составляет с прямой линией, соединяющей эту точку с МЦУ, угол m.

Итак, отношение ускорения любой точки плоской фигуры к расстоянию от неё до МЦУ есть величина постоянная (рис. 33) и равна из (28):

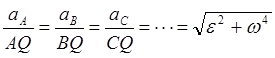. (29)