
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Способы определения положения МЦС.
3a. Пусть известен вектор скорости 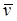 A некоторой точки A плоской фигуры S и угловая скорость w вращения фигуры S вокруг этой точки.
A некоторой точки A плоской фигуры S и угловая скорость w вращения фигуры S вокруг этой точки.
В этом случае положение МЦС определяется так, как это сделано в пункте 1 (рис. 27).
3b. Пусть известен вектор скорости 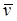 A некоторой точки A плоской фигуры S и направление вектора скорости
A некоторой точки A плоской фигуры S и направление вектора скорости 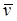 D другой точки D плоской фигуры S (рис. 28).
D другой точки D плоской фигуры S (рис. 28).
В этом случае для определения положения МЦС надо провести из этих точек лучи, направленные перпендикулярно векторам скоростей этих точек. Точка пересечения этих лучей и является МЦС плоской фигуры S (рис. 28).
3c. Пусть известны скорости 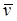 A и
A и 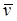 B (или
B (или 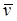 A и
A и 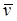 C) двух точек A и B (или A и C) плоской фигуры S. Вектора этих скоростей параллельны между собой и перпендикулярны прямой, соединяющей эти точки (рис. 28).
C) двух точек A и B (или A и C) плоской фигуры S. Вектора этих скоростей параллельны между собой и перпендикулярны прямой, соединяющей эти точки (рис. 28).
В этом случае для определения положения МЦС надо соединить сами точки и концы векторов скоростей этих точек (рис. 28). Точка пересечения проведенных линий и является МЦС плоской фигуры S (рис. 28).
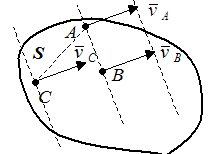 Рис. 29.
Рис. 29.
|
3d. Пусть известны вектора скоростей 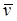 A и
A и 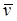 B (или
B (или 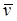 A и
A и 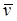 C) двух точек A и B (или A и C) плоской фигуры S. И вектора скоростей этих точек (рис. 29) параллельны между собой и равны (или не перпендикулярны прямой, соединяющей эти точки).
C) двух точек A и B (или A и C) плоской фигуры S. И вектора скоростей этих точек (рис. 29) параллельны между собой и равны (или не перпендикулярны прямой, соединяющей эти точки).
В этом случае МЦС (точка P) плоской фигуры S находится в бесконечно удаленной точке. Из отношения (25) следует, что в этот момент времени угловая скорость плоской фигуры S равна нулю: w=0. Из уравнений (23) и (22) следует, что в этом случае вектора скоростей всех точек плоской фигуры S равны между собой:
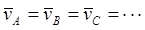 .
.
В этом случае движение плоской фигуры S может быть названо мгновенно поступательным.
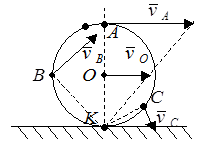 Рис. 30.
Рис. 30.
|
3e. В некоторых случаях положение МЦС удается указать из общих соображений.
Примером может являться качение без проскальзывания диска по неподвижной поверхности. Точка контакта K одновременно принадлежит и неподвижной поверхности и катящемуся диску, следовательно, при качении без проскальзывания она постоянно является МЦС диска. Картина распределения скоростей для этого случая приведена на рисунке 30.
Дата добавления: 2015-04-15; просмотров: 332; Мы поможем в написании вашей работы!; Нарушение авторских прав |