Мгновенный центр ускорений плоской фигуры.

МЦУ плоской фигуры называется точка (неразрывно связанная с плоской фигурой), ускорение которой в данный момент времени равна нулю:

Доказательство существования МЦУ.

Рис. 32.

Пусть известен вектор ускорения 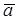_A некоторой точки A плоской фигуры S, угловая скорость w и угловое ускорение e вращения фигуры S вокруг этой точки (рис. 32).

Повернем вектор ускорения 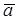_A на угол в сторону углового ускорения e вращения фигуры S и проведем в этом направлении луч из точки A. На проведенном луче отложим (рис. 32) отрезок, равный: .

Из теоремы 4 определим ускорение точки Q: . Так как, согласно (27), , .

Таким образом, доказано существование МЦУ – точки Q, ускорение которой в данный момент времени равно нулю.

Единственность этой точки Q доказывается методом от противного.