Скорость точки при сложном движении.

Теорема 6 (о скорости точки при сложном движении). При сложном движении точки её абсолютная скорость равна векторной сумме переносной и относительной скоростей.

Пусть движение точки O относительно неподвижной системы координат Ox₁y₁z₁ определяется радиус-вектором (рис. 46).

Тогда при сложном движении точки M в любой момент времени выполняется следующее тождество: .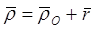

Продифференцируем это векторное тождество по времени:

,

так как 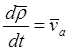– скорости точки M относительно неподвижной системы координат, то есть, её абсолютной скорости; 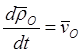– скорости точки O относительно неподвижной системы координат.

.

В последнем выражении были использованы формулы Пуассона:

, , .

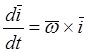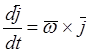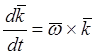Здесь 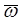– вектор угловой скорости тела D.

И, наконец, 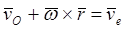– скорости той точки тела D, с которой в данный момент совпадает движущаяся по телу точка M, то есть, переносной скорости точки M. Что и требовалось доказать:

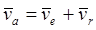. (36)