Ускорение Кориолиса.

Ускорение Кориолиса характеризует изменение вектора относительной скорости точки M в её переносном движении и изменение вектора переносной скорости точки M в её относительном движении.

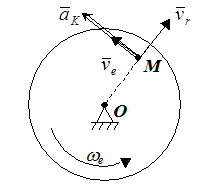Рис. 47.

Поясним последнее утверждение на примере равномерного и прямолинейного движения точки M по радиусу диска от его центра, когда сам диск вращается равномерно (рис. 47).

В приведенном примере изменение направления вектора относительной скорости точки M происходит за счет вращения диска (a_r=0), то есть, при переносном движении точки. Изменение величины переносной скорости происходит за счет перемещения точки M по диску (e_e=0), то есть, при относительном движении. И то и другое характеризует ускорение Кориолиса.

Вектор ускорения Кориолиса равен удвоенному векторному произведению угловой скорости переносного движения точки на линейную скорость её относительного движения:

, (38)

и, следовательно, вектор 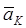направлен по правилу правой руки (рис. 44).

Величина ускорения Кориолиса равна удвоенному произведению угловой скорости переносного движения точки на относительную её скорость и на синус угла между векторами этих характеристик:

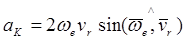. (39)

Отметим случаи, когда ускорение Кориолиса обращается в ноль:

1) w_e=0, то есть, переносное движение является поступательным;

2) v_r=0, то есть, в те моменты времени, когда происходит изменение направления относительного движения;

3) 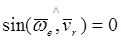, то есть, когда векторы угловой скорости переносного движения и линейной скорости относительного движения параллельны между собой.