
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Численные методы
Общая постановка задачи, например, для трехзвенного манипулятора с тремя вращательными парами формулируется следующим образом. Известны положения схвата в пространстве - начальное Pн, действительное Pд (определенное на i-ом шаге корректировки) и конечное (желаемое) Pж положения, задаваемые декартовыми координатами. Необходимо определить такие значения обобщенных координат qi, 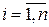 которые обеспечивали бы положение центра схвата в точке Pж (желаемое положение).
которые обеспечивали бы положение центра схвата в точке Pж (желаемое положение).
Поставленная таким образом задача является задачей минимизации функции трех переменных и целевая функция будет иметь вид

| (39) |
где  - радиус – векторы действительного и желаемого положения центра схвата.
- радиус – векторы действительного и желаемого положения центра схвата.
В случае многозвенного манипулятора, когда число степей свободы больше трех необходимо знать еще и ориентацию манипулятора в пространстве. Таким образом, для определения ориентации манипулятора с числом степеней свободы n<3, помимо координат центра схвата, необходимо знать дополнительные параметры, например, положение начала системы координат схвата в базовой системе координат On .Обозначив желаемое положение точки Onкак Onж, получим выражение для целевой функции, учитывающей как положение схвата так и ориентацию манипулятора.
 . .
| (40) |
где 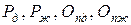 - радиус – векторы действительного и желаемого положения центра схвата, действительного и желаемого положения начала системы координат схвата, то есть точки On.
- радиус – векторы действительного и желаемого положения центра схвата, действительного и желаемого положения начала системы координат схвата, то есть точки On.
Таким образом, необходимо минимизировать функцию  , задавшись точностью, и определить минимум функции.
, задавшись точностью, и определить минимум функции.
Целевая функция (40) представляет собой нелинейную функцию многих переменных, содержащую тригонометрические зависимости, отклик которой - это сложная гиперповерхность с наличием впадин, седловых точек, овражностей. Такую поверхность невозможно представить геометрически. Сложность, таким образом, возникает в определении глобального минимума функции среди множества локальных.
В целом все практически используемые методы являются методами локального поиска. Надежные и одновременно экономичные методы поиска глобального минимума в настоящее время неизвестны.
Существующие методы оптимизации классифицируются в зависимости от 1) типа искомого экстремума (минимума)- методы локальной и глобальной оптимизации; 2) порядка используемых производных целевой функции по управляемым параметрам – методы нулевого, первого и второго порядка; 3) количества управляемых параметров целевой функции – методы одномерного и многомерного поиска.
Среди методов многомерного поиска нулевого порядка выделяют методы деформируемого многогранника (Нелдера и Мида), покоординатного спуска, метод Рзенблата, метод случайного поиска. К методам первого порядка относят градиентные методы: метод наискорейшего спуска, метод сопряженных градиентов, метод переменной метрики. Метод Ньютона является методом второго порядка.
Практически все методы оптимизации стремятся построить такую последовательность значений q0, q1, q2, и т.д. при которой f(q0) > f(q1) > f(q2) >…,. В этом случае метод обеспечивает сходимость и можно надеяться, что минимум функции будет найден.
Важно характеристикой методов является их скорость сходимости. Однако оценка сходимости того или иного метода обычно базируется на некоторых теоретических предпосылках относительно особенностей целевой функции (например, функция дважды непрерывно дифференцируема или сильно выпукла), а также зависит от выбора начальной точки поиска. Теоретические предпосылки относительно реальных целевых функций могут не удовлетворяться, поэтому скорость сходимости в этих случаях можно рассматривать как сравнительную оценку метода.
Численные методы позволяют построить последовательность шагов от начальной точки q0 через некоторые промежуточные тоски qk к локальному экстремуму (минимуму) q*. Как отмечалось выше, выбор исходной точки поиска q0 во многом определяет успех решения всей задачи. Очевидно, что q0 должна принадлежать области определения целевой функции и, чем ближе к экстремуму выбрана q0, тем быстрее и с большой вероятностью экстремум будет найден. Сущность метода оптимизации определяется этапами 2 и 3 алгоритма, на которых выбирается направление дальнейшего поиска и вычисляются координаты очередной точки qk+1 на траектории поиска. Далее в точке qk+1 вычисляются значения целевой функции f(qk+1), т.е. определяется информация, позволяющая судить о достигнутом успехе. В зависимости от выполнения назначенных условий прекращения поиска поиск будет продолжен или прекратиться.
Численный метод позволяет решить обратную задачу кинематики для тех конструкций манипуляторов, для которых получение точного решения в аналитических выражениях не представляется возможным, либо достаточно затруднительно. Это является основным достоинством при использовании численного метода применительно к поставленной задаче.
Кроме того, численные методы решения обратной задачи позволяют достичь требуемой точности решения. Однако время сходимости того или иного метода заранее неизвестно и во многом зависит от начального приближения. В результате чувствительность к количеству переменных целевой функции, виду гиперповерхности, а также различная скорость сходимости и потери на поиск требуют значительных вычислительных мощностей, что затрудняет их использование в реальном времени.
5. Приложение 1. Пример использования
различных кинематических параметров
 Решается прямая задача кинематики о положении манипулятора на примере робота-манипулятора PUMA-260 [1], кинематическая схема которого представлена на рис. 8 (в рассмотрение взяты три вращательные кинематические пары).
Решается прямая задача кинематики о положении манипулятора на примере робота-манипулятора PUMA-260 [1], кинематическая схема которого представлена на рис. 8 (в рассмотрение взяты три вращательные кинематические пары).
5.1. Матрицы
направляющих косинусов
Матрицы перехода от одного звена манипулятора к другому составляются в соответствии с элементарными поворотами при совмещении  и
и  систем координат.
систем координат.
Таким образом, смещение системы координат 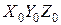 в
в  осуществляется с помощью двух поворотов:
осуществляется с помощью двух поворотов:
1) поворот на  вокруг оси
вокруг оси 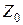 (матрица
(матрица  ),
),
2) поворот на  вокруг оси
вокруг оси  (матрица
(матрица  ).
).
Результирующая матрица перехода от одной системы координат к другой имеет вид:
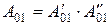 , где , где
| |
 , ,  , ,
|
откуда
 . .
| (41) |
Совместим теперь систему координат  с
с  , вращая первую систему координат вокруг оси
, вращая первую систему координат вокруг оси  на угол
на угол  (матрица
(матрица  )
)
 . .
| (42) |
И таким же образом получим матрицу перехода от системы координат  и
и  , повернув систему координат
, повернув систему координат  :
:
1) вокруг оси  на
на  (матрица
(матрица  ),
),
2) вокруг оси 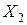 на
на  (матрица
(матрица  ).
).
Матрицы элементарных поворотов  и
и  имеют вид, матриц поворотов, составленных при переходе от основания к первому звену манипулятора. То есть, можно записать, что результирующая матрица перехода
имеют вид, матриц поворотов, составленных при переходе от основания к первому звену манипулятора. То есть, можно записать, что результирующая матрица перехода  определяется как
определяется как

| (43) |
После получения всех трех матриц  ,
,  и
и 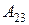 , последовательно перемножая их, получим в результате будем иметь матрицу, связывающую систему координат основания
, последовательно перемножая их, получим в результате будем иметь матрицу, связывающую систему координат основания  с системой координат последнего звена манипулятора
с системой координат последнего звена манипулятора  .
.
 , ,
|
После тригонометрических преобразований получим
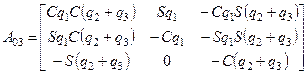 . .
| (44) |
Дата добавления: 2015-04-15; просмотров: 363; Мы поможем в написании вашей работы!; Нарушение авторских прав |