Параметры Кейли-Клейна

Параметры Кейли-Клейна представляют собой комплексно-сопряженные комбинации параметров Родрига-Гамильтона, составляющих кватерниона, и имеют вид

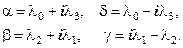
(55)

Матрица перехода между соседними звеньями (66) составлена из элементов (65)

.

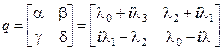(56)

Таким образом, в результате последовательного перемещения от одного звена к другому будут получены матрицы перехода вида (56), которые будучи перемноженными между собой в том же порядке дадут результирующую матрицу, связывающую основание манипулятора с последним звеном.

При совмещении систем координат выше были получены кватернионы, соответствующие элементарным плоским поворотам. Их и будем использовать для составления матриц перехода. Переход ® можно описать двумя кватернионами: ; 2) .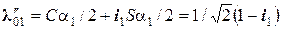

В результате чего можно составить две матрицы перехода

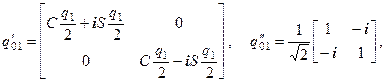
	(57)

Переход ® описан через кватернион вращения 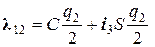, откуда

.

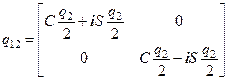(58)

Так как при переходе от системы координат к кватернион аналогичен кватерниону , то получим

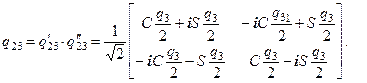
(59)

В результате перемножения полученных матриц перехода (56) - (59), результирующая матрица будет иметь вид:

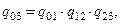
и в окончательном виде, получим:	(60)