Решение задач

2. элементы ВЕКТОРНой АЛГЕБРы

ЗАНЯТИЕ 1.

Тема: ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ

Задание 1

1) Если векторы и 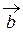коллинеарны, то следует ли отсюда что они сонаправлены? Если два вектора а и b сонаправлены, то следует ли отсюда что они коллинеарны? 2) Справедливо ли предложение: если вектор коллинеарен вектору , то вектор коллинеарен вектору и вектор коллинеарен вектору ?

3) Следует ли из равенства векторов = равенство отрезков AB = CD? Следует ли из равенства отрезков AB = СD равенство векторов = ?

4) Могут ли у двух равных векторов начала совпадать, а концы - нет?

5) Может ли нуль вектор быть равен какому-нибудь ненулевому вектору?

6) Могут ли два вектора, лежащие на перпендикулярных прямых, быть: а) коллинеарными, б) равными?

7) В пространстве даны три вектора, среди которых два - коллинеарны. Можно ли утверждать, что все три вектора компланарны?

8) В пространстве даны два вектора и 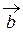. Всегда ли можно выбрать третий вектор , 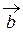и были: а) компланарны; б) не компланарны?

9) Может ли модуль разности двух векторов быть больше как модуля
вычитаемого, так и модуля уменьшаемого?

10.Мы должны знать, что векторные величины характеризуются абсолютным значением (модулем), направлением и геометрическим способом сложения - это самое важное в определении вектора, так как не все физические величины, имеющие модуль и направление, являются векторными. Например, сила тока имеет модуль и направление, но является скалярной величиной.

Задание 2: Выполнить действия над векторами геометрическими методами.

Пример 1 . Даны три вектора:

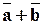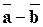Найти: 1) ;2) ; 3) ; 4) .

Решение:

1) - сложение двух векторов геометрически выполняется:

а) методом треугольника:

б) методом параллелограмма:

2) - сложение трех векторов геометрически выполняется

методом многоугольника:

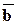
3) 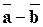-вычитание векторов геометрически выполняются:

а) методом треугольника или параллелограмма:

б) методом треугольника с использованием противоположного вектора ( ),при этом вычитание заменяется на сложение векторов: = :

=

4) -умножение векторов на числа геометрически приводит к удлинению вектора ā в 2 раза, к укорочению вектора 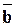в 3 раза, а также к смене направления вектора на противоположное. Результирующий вектор , идущий из начала первого в конец последнего, находится методом многоугольника.

2*

-

Задание 3: Выполнить действия над векторами аналитически с помощью координат.

Пример 2.Даны векторы

.

Решение:

;

;

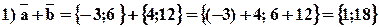Пример 3. Даны 3 точки А(6;-2), В(-3;1), С(2;0). Найти векторы 1) 3)

Решение:

1.Найдем координаты векторов:

2.Выполним операции над векторами:

1)

2)

Пример 4. Найти равнодействующую двух сил и и построить векторы.

1.Найдем равнодействующую силу как сумму векторов:

2.Построим векторы по координатам.

Самостоятельная работа

Задание1:Выполнить линейные операции над векторами.

1. Даны векторы:

Найти: 1) ; 2) ; 3) ; .

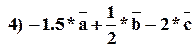2. Даны векторы: Найти: 1) ; 2) ; 3) ; .

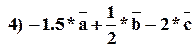2. Даны три точки А(-1;1), В(3;-2), С(2;4). Найти векторы 1) 3)

3. Найти равнодействующую трех сил: и построить векторы.

ЗАНЯТИЕ 2.

Тема: ОПРЕДЕЛЕНИЕ МОДУЛЯ ВЕКТОРА И ЕГО НАПРАВЛЕНИЯ В ПРОСТРАНСТВЕ. СКАЛЯРНОЕ И ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

Пример 1. Даны на плоскости точки А(-2;3) и В(2;7). Найти 1) вектор , 2) модуль , 3) направляющие косинусы, 4) построить вектор .

Решение:

1.найдем координаты вектора:

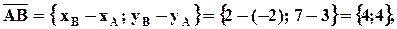выпишем егокоординаты АВ_х = 4, АВ_у= 4;

2.вычислим модульпо формуле: ;

3.вычислим направляющие косинусы по формулам:

4) построим векторпо его координатам

и координатам точек А(-2;3) и В(2;7).

Пример 2. Найти проекцию вектора на вектор .

Решение:

Пример 3. Определить работу по перемещению тела из точкиА(2;-4;1)в точкуВ(3;2,-1)под действием сил: .

Решение:

1.Найдем вектор перемещения тела:

;

2.Вычислим равнодействующую трех сил:

.

3.Определим работу по перемещению тела, как скалярное произведение вектора равнодействующей силы и вектора перемещения:

А= = 4*1+6*6+(-2)*3=34 ед. работы.

Пример 4. Вычислить площадь треугольника с вершинами: А(3;1;2), В(4;3;5) и С(-8;2;3).

Решение:Так как ,

1.Найдем координаты векторов:

;

2.Определим векторное произведение:

=

3.Вычислим площадь треугольника:

кв. ед.

Самостоятельная работа

Задание 1.

1.Даны на плоскости точки М(3;-2) и N(-1;3). Найти 1) вектор , 2) модуль , 3) направляющие косинусы, 4) построить вектор .

2.Найти проекцию вектора на вектор .

3.Определить работу по перемещению тела из точки А(1;3;-2) в точку В(2;-1;4) под действием сил: .

4.Вычислить площадь треугольника с вершинами: А(-1;2;4), В(1;3;6)иС(-3;5;2).