АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

ЗАНЯТИЕ 1 и 2.

Тема: ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ

Пример 1.Даны две точки А(-1;2) и В(1;5). Найти: 1) длину АВ; 2)С(х_с;у_с) –середину АВ; 3)записать уравнение прямой АВ, 4)найти k- угловой коэффициент и b-отрезок оси Оу, отсекаемый прямой.

Решение:

1.Длина АВ= ;

2.Координата С(х_с;у_с)–середины АВнайдем по формуле:

. С(0;3.5) –середина АВ;

3.Запишем уравнение прямой, проходящей через две заданные точкиАиВ: .

Подставим координаты точек А(х_А = -1, у_А = 2)иВ(х_В = 1, у_В = 5) в это уравнение: 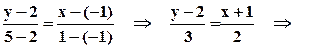2(у - 2) = 3(х + 1) 2у - 4 = 3х + 3 -3х + 2у - 7 = 0.Получилиобщее уравнение прямой АВ.

4.Преобразуем полученное уравнение в уравнение прямой с угловым коэффициентом вида:у=кх+b. Выразим учерез х:2у=3х+7 /:2 у = (х +7) 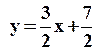- это уравнение прямой АВ с угловым коэффициентом, где - угловой коэффициент АВ, а b= 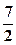--отрезок оси Оу, отсекаемый прямой.

Угловой коэффициент прямой, проходящей через две заданные точкиАиВ можно рассчитать по формуле: .

Пример 2. Записать уравнение прямых, проходящих через точку С(-4;2) параллельно и перпендикулярно прямой, проходящей через точки А(3;-4) и В(2 -2).

Решение:

1.Найдем угловой коэффициент для прямой АВ:

.

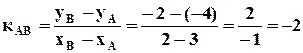2.Найдем угловой коэффициент для прямой 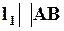из условия параллельности: .

3.Найдем угловой коэффициент для прямой из условия перпендикулярности: .

4.Запишем уравнения прямых и , используя уравнение прямой, проходящей через заданную точку С с заданными угловыми коэффициентами:

;

.

Пример 3. Дан треугольник с вершинами А(-8;3), В(-6;0), С(6;-5). Составить уравнения 1) стороны АС, 2) высоты CD и 3) медианы ВЕ. 4) Найти координаты точки М(х_м;у_м) – пересечения высоты CD и медианы ВЕ.

Решение:

1. Составим уравнение стороны АС,используя уравнение прямой, проходящей через две заданные точки:

Þ Þ Þ 14*(у - 3)=(-8)*(х + 8) Þ

8х + 14у + 22=0 – искомое уравнение стороны АС;

2. Высота CD АВÞ .

Найдем и

Составим уравнение высоты CD,используя уравнение прямой, проходящей через заданную точку С(6;-5) с заданным угловым коэффициентом : 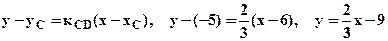- искомое уравнение высоты CD с угловым коэффициентом. Запишем его в общем виде, умножив обе части уравнения на 3: 2х-3у-27=0- общее уравнение высоты CD;

3. Медиана ВЕ проходит через середину стороны АС.Найдем координаты Е(х_Е;у_Е)-середины отрезка АС по формулам: . Е (-1;-1)-середина стороны АС.

Составим уравнение медианы ВЕ, используя уравнение прямой, проходящей через две заданные точки:

Þ Þ Þ 5у =-х-6 Þ

х + 5у + 6=0 – искомое уравнение медианы ВЕ;

4. Найдем координаты точки М(х_м;у_м) – пересечения высоты CD и медианы ВЕ, решив систему их уравнений методом Крамера:

• Вычислим определители системы и неизвестных D, D_х, и D_у.

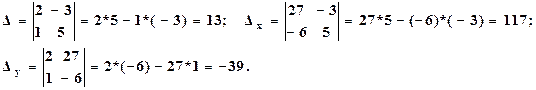
• Найдем решение системы по формулам Крамера:

х_М ; у_М =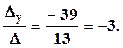

Проверка: 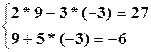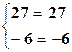(верно).

М (9;-3) -точка пересечения высоты CD и медианы ВЕ.

Самостоятельная работа

Задание 1.

1.Даны две точкиМ(2;-3) и N(4;5).Найти: 1) длинуMN; 2)С(х_с;у_с) –середину MN; 3)записать уравнение прямойMN, 4)найти k- угловой коэффициент и b-отрезок оси Оу, отсекаемый прямой.

2. Найти уравнение прямой, параллельной прямой 4х - 6у - 8 = 0 и проходящей через точку (3; -1).

3. Найти уравнение прямой, проходящей через точку (—2; 3) пер­пендикулярно к прямой —5х + 7у + 2 = 0.

4. Составить уравнения прямых, проходящих через заданную точку K(-1;3) параллельно и перпендикулярно прямой, заданной уравнением: 2х+4у-3=0.

5. Найти угол между прямыми 3х + у— 5 = 0 и у = 2х + 4.

6.Даны прямые 2х — 3у + 7 = 0 и х + 2у — 3 = 0. Найти угол между ними. Изменится ли величина этого угла, если в заданных уравнениях изменить значения свободных членов C = 7 и С = - 3, взяв, например, С = - 5 и С = + 8?

7. Треугольник ABC задан координатами своих вершин А(— 1; —3), 1), С (2; 5). Найти уравнение высоты, опущенной из вершины С

8. Треугольник М М М задан координатами своих вершин М (5;6), М (1; 2); М (7; 4). Найти точку пересечения его медиан.

* Эта точка совпадает с центром тяжести треугольника, точнее, треугольной пластины постоянной толщины, вырезанной из однородного материала.

9.Найти точку пересечения каждой из следующих пар прямых:

а) 3х — 5у + 10 = 0 и 2х + 7у — 8 = 0,

б) 3х — 5у + 4 = 0 и 6х — 10у — 15 = 0,

в) — 7х + 2у— 12 = 0 и 4х— 11у + 13 = 0.

10.Дан треугольнике с вершинами М (2;5), N(-3;6), K(4;-3). Записать уравнения 1) стороны MK, 2) высоты KD и 3) медианы NЕ, 4) Найти координаты точки P(х_p;у_p) – пересечения высоты KD и медианы NЕ.

11. Треугольник М М М задан координатами своих вершин М (-3; 4), М (4; 3), М (0; -5). Определить точку пересечения перпендикуляров, проходя­щих через середины сторон.

ЗАНЯТИЕ 3.

Тема: ЛИНИИ ВТОРОГО ПОРЯДКА

Пример 1. Привести к каноническому виду, определить параметры и построить линию, заданную уравнением: 4х² + у² + 24х - 4у + 4 = 0.

Решение:

1)Приведем уравнение к каноническому виду. Для этого сгруппируем члены с координатами хиуи дополним их до полных квадратов:

4(х²+2*3х+9-9)+(у²-2*2у+4-4)+4=0 Þ 4(х+3)²-36+(у-2)²-4+4=0 Þ

4(х+3)²+(у-2)²=36.Разделим обе части уравнения на 36 и получим каноническое уравнениелинии:

.

Это эллипс со смещенным центром вида:;

2)Найдем параметры: -малая полуось на оси Ох;

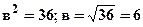- большая полуось на оси Оу;

- фокусное расстояние;

e= 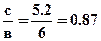- эксцентриситет.

Фокусы F₁(0;5.2) и F₂(0;-5.2) лежат на большой оси, совпадающей с осью ординат Оу, симметрично на расстоянии ±с=±5.2 относительно начала координат.

Найдем координаты смещенного центра С(х₀;у₀): х-х₀=х+3, тогда х₀ = -3;

у-у₀=у-2, тогда у₀ = 2,следовательно С(-3;2) – смещенный центр.

3)Для построения эллипса перейдем к вспомогательной системе координат Сх₁у_1, приняв за новые координаты: х₁=х+3; у₁=у-2. Тогда во вспомогательной системе координатполучим уравнение эллипса с несмещенным центром: .

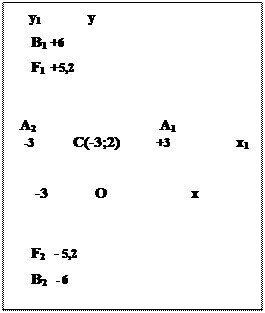
Этапы построения такого эллипса с несмещенным центром во вспомогательной системе координат аналогичны вышеописанным этапам предыдущего примера:

· строим основную и вспомогательную системы координат Оху иСх₁у₁;

· на координатных осях вспомогательной системы откладываем симметрично относительно начала координат малую и большую полуоси (±а=±3, ±в=±6) и показываем вершины эллипса А₁,А₂,В₁,В₂;

· через вершины эллипса параллельно координатным осям строим осевой прямоугольник;

· вписываем эллипс в осевой прямоугольник;

· на большой оси, совпадающей с осью Су₁, симметрично относительно начала координат на расстоянии ±с=±5.2показываем фокусы F₁(0;5.2) и F₂(0;-5.2).