Сущность физико-математических понятий

Раскроем сущность этих понятий.

Понятие, вообще, определяется как форма научного знания, в которой в обобщением виде раскрываются наиболее существенные при­знаки явлений, объектов и процессов.

Математика создает понятия с целью отображения только фор­мы систем действительности, абстрагируясь от их содержания как от несущественных для математического отображения действительно­сти. Математические абстракции описывают количественные отношения объектов, отвлекаясь от их физической природы. В резу­льтате такого отвлечения - объектом изучения становится чистая количественность, понятие количества. Например, явление свобод­ного падения, выраженное физическим законом S= gt 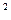/2 , где S - путь, t - время, g - ускорение силы тяжести и внутреннее состояние тела, описанное законом Е = mv 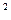/2, где m - масса, v - скорость, в математике отражается в функции вида у = ax 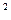/2, где x,y и а - означают не конкретные физические свойства явлений и процессов, а переменные количества и числа вообще.

Математические закономерности (например, если у=f(x)), то dу=f (x) dx) объективны, но они не существуют как та­ковые наряду с реальными явлениями и процессами. Они существуют только через количественные характеристики конкретных материаль­ных процессов и состояний, которые в свою очередь функционируют в рамках действия объективных математических закономерностей.

Физические понятия отражают содержание реальных предметов, с помощью обобщения и переработки информации, полученной через чувственное восприятие. Понятия физика, таким образом, отражают качественные характеристики реальных объектов и явлений. Напри­мер, к ним относятся понятия, описывающие строение вещества (молекулярно-кинетическая, электронная и квантовая теории, тео­рия строения атома и ядра), законы сохранения (энергии, импуль­са, заряда, массы), волновые и корпускулярные свойства света, гравитационное и электромагнитное поле.

Таким образом, математика и физика изучают физические закономерности явлений и процессов реальности. Причем особенности физических и математических понятий состоят в том, что физические понятия отражают непосредственно материальный предмет или систему предметов, а также реально существующие связи и взаимо­действия между ними, а математические понятия отражают ту же реальность, но опосредованно, через свои специфические объекты, которые реально в окружающем вас мире не существуют,

Специфические особенности математических понятий позволяют понять количественные характеристика и структурные особенности изучаемого физического явления или процесса. Но абстрактность математических понятий в конкретизации физических понятий порож­дают трудности в освоении связей и отношений существующие между этими понятиями.

Для раскрытия существующих связей и отношений между физиче­скими и математическими понятиями синтезируют существенные признаки этих понятий, выбирая за основание либо математический признак, либо физический признак, либо физико-математический признак. Такие понятия будем называть физико-математическими.

Под физико-математическим понятием будем понимать такое по­нятие, которое отражает одновременно как физическую качественную, так и математическую (количественную) сущности некоторого явления или процесса, протекающих в природе.

Мы рассмотрим два физико-математических понятия - "функция" и "производная".

В физике и технике происходят различные процессы и изменения. Они описываются в математике функциями, которые отражают сложность этих процессов и явлений, а также взаимных зависимостей между ними.

Под физико-математическим понятием "функция" будем понимать математические способы выражения зависимостей одних физических величин от других физических величин, где переменные и параметры, входящие в аналитическое выражение, имеют некоторое физическое наполнение.

Большое разнообразие физических явлений и процессов породи­ло и многообразие функциональных зависимостей, отражающих закономерности течения этих явлений и процессов.

Другим важным физико-математическим понятием является "производная". Под физико-математическим понятием "производная" бу­дем понимать переменную величину, которая характеризует количе­ственные изменения одной физической величины в зависимости от другой физической величины в каждой точке существования послед­ней и, определяемая как предел отношения количества первой фи­зической величины к количеству второй, когда последнее стремит­ся к нулю. Иначе говоря, производная характеризует скорость про­текания того или иного процесса или явления в данный момент вре­мени.

Физико-математические понятая "функция" и "производная" описывают движения материи, текущие процессы, непрерывно изменяющиеся состояния. Поэтому важно при освоении математической сущности этих понятий одновременно освоить и их физическое содержание.

Рассмотрим физико-математические сущности этих понятий.

2.2. Виды и техническая интерпретация физико- математического понятия "функция"

Качественные стороны физических явлений и процессов взаимо­связаны с количественными соотношениями, которые характеризуют то или иное явление. Количественные соотношения между физически­ми величинами устанавливаются экспериментальным путем и выражаются в форме математического уравнения; функции и т.п. Поэтому будущему инженеру при освоении математических функций важно понимать их физический смысл, чтобы правильно использовать физи­ческое явление, процесс в конструировании технического устройст­ва или технологического процесса.

Рассмотрим, каким может быть физическое содержание математического понятия "функция", т.е. каков физический смысл параметров и переменных, входящих в аналитическое выражение функции.

Начнем с рассмотрения элементарных функций. Первая из них "линейная функция" - у = кх + b, где к и b - параметры, а х и у - переменные.

Из математики известно, что сущность линейной зависимости состоит в том, что одинаковым приращениям аргумента X всегда соответствует одно и тоже приращение функции.

Особого доказательства требует обратное утверждение, а именно, если равным приращениям аргумента (считая от любого его начального значения) соответствуют равные при­ращения функции, то эта функция линейная.

Процесс, в котором зависимость одной величины от дру­гой описывается линейной функцией, называется равно­мерным. В таком процессе равным изменениям одной вели­чины соответствуют равные изменения другой величины. Равномерные процессы широко распространены в при­роде и технике.

Например, равномерно накапливается во­да в цилиндре, поставленном под водопроводный кран, ес­ли струя создается неизменным напором; это значит,- что за равные промежутки времени, считая от любого началь­ного момента, в цилиндр поступают равные объемы воды.

Равномерность действия, процесса может рассматри­ваться не только по отношению ко времени. Так, например, в пружинных весах пружина изменяет свою длину под дей­ствием изменяющейся нагрузки равномерно; это значит, что равным изменениям нагрузки (веса), считая от любого начального значения, соответствуют равные изменения дли­ны пружины.