Применение метода линейного программирования для решения задач управления

Фирма, работающая в условиях того или иного типа рынка, должна воспринимать его как общие условия своего функ­ционирования и в соответствии с ними выстраивать общую ли­нию (стратегию) поведения на рынке. Вместе с тем при реализа­ции этой стратегии она может сталкиваться с множеством более или менее сложных проблем, которые также могут быть иссле­дованы и решены с помощью соответствующих моделей. Так, если все факторы проблемы заданы однозначно, известны также взаимосвязи между ними и результирующими показателями, для разрешения производственных трудностей можно исполь­зовать модели, решение которых отыскивается с помощью ме­тода линейного программирования (МЛП). Основная область применения МЛП - поиск оптимального распределения ограни­ченных ресурсов при наличии конкурирующих потребностей. Типичные ситуации, в которых можно применять линейное программирование:

• составление номенклатуры товаров, запланированных к производству, минимизирующей общие издержки при ограничениях на трудовые ресурсы и уровни запасов;

• определение оптимального маршрута доставки товаров, а в более общем случае - продвижения продукта по точкам технологической цепи;

• определение оптимального сочетания продуктов на складе;

• определение оптимального местоположения нового предприятия с учетом ограничений на расход кабеля или минимизации капитальных затрат;

• распределение работников по рабочим местам для минимизации общих производственных издержек;

• календарное планирование: составление календарных планов с учетом расходов на содержание запасов, оплату сверхурочных работ и заказов на стороне с целью минимизации затрат и т.д.

В названии метода отражены его характерные особенно­сти. Линейное — так как все компоненты модели представляются и виде линейных неравенств или уравнений. Программирование, так как отыскивается наилучшая программа действий при иных условиях и ограничениях.

Метод линейного программирования, впервые сформулированный Л.В.Канторовичем, является одним из наиболее развитых методов исследования операций. Общий метод решения задач линейного программирования — симплекс-метод, который разработан американским ученым Дж.Данцигом.

Общая задача линейного программирования может быть сформулирована следующим образом. Необходимо отыскать неизвестные х₁, х₂,..., , х_j,..., х_п> при которых достигается максимум (минимум) линейной функции (цели) задачи

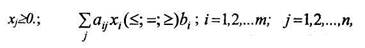
где a_ij,b_j,c_j —заданные величины.

Все ограничения представляют собой многогранник условий, существующий в m-мерном пространстве. Решение заклю­чается в том, что одна из вершин выбирается в качестве опор­ной, а затем в соответствии с определенной процедурой на ос­нове однотипных расчетов исследуются другие вершины много­гранника условий так, чтобы решение на каждом шаге улучша­лось (увеличивалось или уменьшалось значение целевой функ­ции). Если задача имеет решение, то за конечное число итера­ций (без перебора всех вершин) можно найти наилучшее с точки фения выбранного критерия решение.

Рассмотрим в общем виде задачу линейного программирования. Пусть планируется производство различных видов ус­луг У₁, У₂,.., У_п. Считается, что рынок предъявит спрос на каж­дую услугу в размере не больше, чем q₁ q₂,..., q_n..

Для производства этих услуг требуются различные виды ресурсов R₁,R₂,..., R_m в количестве единиц не больше, чем b₁ ,b₂ ,...,b_т.. Для производства услуги i-го вида требуется a_ij единиц-j-го вида ресурсов. При этом предполагается продавать услуги по ценам p₁, а себестоимость единицы услуги е₁, т.е. прибыль от каждой единицы услуги составит с_i =p_i,— е_i.

Таким образом, требуется произвести объем услуг, не превышающий спрос по каждой услуге так, чтобы получить максимум прибыли при имеющихся ресурсах.

Модель задачи имеет следующий вид:

1) х_i - количество услуг i-гo вида, подлежащее определению;

2)x_i≥0;

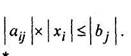
3)x_i≤q_i.

4)В матричной форме

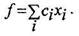
Найти оптимальные х_i^* (i=1, 2,..., п), которые удовлетворяют системе ограничений 1—4 и обращают в максимум целевую

функцию

Линейное программирование может применяться и для решения задач динамического характера, в которых рассматривается конечное число периодов времени, и результаты преды­дущего периода определяют исходные параметры следующего. Несмотря на то, что по сути своей задачи линейного програм­мирования относятся к классу детерминированных, в ряде слу­чаев их можно использовать и для решения задач, постановка которых в явном виде содержит информацию вероятностного характера. Основной прием в этих ситуациях — постараться ввести соответствующие случайные изменения к эквивалентным детерминированным соотношениям, например, вместо распре­деления вероятностей появления различных значений случайной величины использовать средние значения.

Метод линейного программирования имеет ограничения: линейность всех соотношений; необходимость в каждый момент времени оперировать только одним набором ограничений.

Весьма часто влияние экономических факторов на результаты деятельности не может быть описано с помощью линейных соотношений, например, когда затраты на производство продук­та растут медленнее, чем его объемы, или выручка от реализа­ции продукта зависит от цены и спроса на продукт, который, в свою очередь, также зависит от цены.

Для описания таких систем, когда эффективность системы возрастает или убывает непропорционально изменению масштабов производства, приходится прибегать к нелинейной фор­мулировке ограничений или целевых функций. К задачам нели­нейного программирования обычно относят задачи следующего типа: требуется оптимизировать f(х₁, х₂, ..., x_i ..., x_n,) при ограни­чениях:

Естественно, за введение нелинейности в модели приходится платить дополнительную цену: увеличение объема вычис­лительных операций при том, что нельзя назвать два—три эф­фективных алгоритма, как в линейном программировании, для решения любых нелинейных задач. Весьма эффективный в од­ном случае алгоритм может оказаться совершенно непригодным в другом. Вместе с тем все большая доступность машинных программ решения нелинейных задач большой размерности, предназначенных для подготовки решений в сложных ситуаци­ях, улучшающаяся подготовка руководителей и специалистов в области исследования операций способствует развитию теории нелинейного программирования и более широкому использова­нию в практических целях.