
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методы экспертных оценок. Как указывалось ранее, для использования количественных методов прогнозирования необходимо располагать информацией
Как указывалось ранее, для использования количественных методов прогнозирования необходимо располагать информацией, представленной в форме определенных показателей, достаточной для выявления тенденций или статистически достоверной зависимости между переменными. Когда количественная модель оказывается чрезмерно громоздкой или руководитель ее не понимает или нет релевантной информации для целей прогнозирования будущего (состояния рынка, направления развития техники в данной отрасли, целей организации и т.п.), можно использовать различные методы экспертных оценок.
Сущность методов экспертных оценок заключается в проведении экспертами интуитивно-логического анализа проблемы с количественной оценкой суждений и формальной последующей обработкой результатов специалистами-аналитиками. Получаемое в результате обработки по той или иной методике обобщенное мнение экспертов принимается как решение проблемы. При этом предполагается, что опыт экспертов, накопленные знания, интуиция достаточны для решения данной прогнозной задачи. Однако существует опасность, что в особо сложных ситуациях мнение одного эксперта, значительно отличающееся от остальных. Даже если оно будет «истинно», то будет отвергнуто из-за процедуры усреднения мнений экспертов и отбрасывания наиболее отличных мнений от усредненного.
В процессе прогнозирования эксперты в принципе могут выполнять две основные функции:
• формировать альтернативные ситуации, цели, решения, возможные исходы тех или иных проектов и т.д.;
• давать оценки характеристик событий: вероятность их свершения, значимость по отношению к другим, конкретные значения оцениваемых величин.
При использовании метода экспертных оценок возникают такие проблемы, как: подбор экспертов; организация процедуры экспертизы; проведение опроса; обработка результатов опроса экспертов.
Наиболее простые (но не самые эффективные) методы оценок - это дискуссия и совещание по проблеме. При этом решение может быть принято на основе голосования (простым большинством голосов или так называемым «квалифицированным», т. е. проголосовать должно не менее 75% имеющих право голоса или присутствующих) или на основе достижения общего согласия.
Если организация нуждается в новых идеях и альтернативах, можно использовать процедуру «мозгового штурма». При этом до участников обсуждения заранее доводятся цели и задачи процедуры, доступная информация о возможных путях решения проблемы. В ходе обсуждения (около 20 минут, если больше, то участники начинают повторяться) разрешается высказывать самые невероятные идеи, которые запрещается критиковать. Материал фиксируется на пленку, затем обрабатывается специалистами-аналитиками с целью отбора двух - трех наиболее перспективных идей. Для реализации метода требуются много времени, специально подготовленные для проведения «штурма» люди, но зачастую другим методом идей получить не удается.
При изучении спроса на рынке часто используются различные методы опроса потребителей (интервьюирование и анкетирование), когда опрашиваемых просят ответить на ряд вопросов, которые бывают, как правило, трех типов. Первые, так называемые «закрытые», когда требуется ответить «да» или «нет». Но здесь есть опасность уже самим вопросом навязать эксперту ответ. Вторые, с веером ответов, когда против того, с чем потребитель согласен, он ставит «галочку». Третий тип вопросов - свободные, без заранее предлагаемых ответов. Но, как показывает практика, люди не любят работать с белым листом и предпочитают второй тип вопросов с возможностью дополнительных предложений.
В более сложных случаях от экспертов требуется сравнивать какие-то объекты по выбранным показателям с целью установления отношений типа «лучше», «хуже», одинаковы или эквивалентны, предпочтительны, «меньше», «больше», «равны» и т.п. При этом к наиболее употребительным методам измерений относятся ранжирование, парное сравнение, непосредственная оценка, последовательное сравнение.
При использовании каждого из этих методов предполагается, что имеется конечное число сравниваемых объектов О1, О2,.., Оп и есть один или совокупность показателей (признаков), по которым эти объекты сравниваются: J1, J2, …, Jk.
Ранжирование представляет собой процедуру упорядочения объектов в порядке возрастания (или убывания) какого-либо признака (признаков). Если среди объектов нет одинаковых по сравниваемым показателям, т.е. нет эквивалентных объектов, то между ними существуют отношения строгого порядка, которые в практике ранжирования чаще всего отражаются с помощью натуральных чисел r1, r2,…,rn. Эти числа называются рангами. Наиболее предпочтительному объекту присваивается первый ранг, второму - второй и т.д. Если же среди объектов есть эквивалентные с точки зрения рассматриваемых признаков, то этим объектам назначаются одинаковые (связанные) ранги, которые определяются как среднее арифметическое суммы мест, поделенных объектами. Ранжирование позволяет выбрать из исследуемой совокупности явлений наиболее существенное, значимое (или наоборот, чреватое наибольшими потерями, риском). При этом совершенно не обязательно, чтобы изучаемые альтернативы имели одинаковую природу и, следовательно, одинаковую меру непосредственного сравнения. Относительные оценки с помощью рангов позволяют провести такое сравнение. Кроме того, ранжирование может применяться тогда, когда качественные характеристики не могут быть измерены точно или когда какой-то показатель в принципе измерим, однако в настоящий момент времени это не может быть сделано по причинам технического или теоретического характера. Например, требуется оценить следующие объекты с точки зрения их влияния на подготовленность студентов по курсу:
1. Качество лекций: содержание и кто их читает.
2. Качество проведения практических занятий.
3. Самостоятельная работа студента с литературой.
4. Научная работа на кафедре.
5. Консультации с преподавателем в ходе выполнения самостоятельных работ.
6. Посещаемость занятий.
Пусть эти 6 объектов (i=1,..., 6) оценивали 5 экспертов, каждый из которых проранжировал объекты так, как показано в табл. 4.1.
Таблица 4.1
| Экс-пер-ты J=1, …,m | Ранги по степени влияния на обучение для объектов i=1,…,n | |||||
| 1(1) | 2(2.5) | 3(5) | 3(5) | 2(2.5) | 3(5) |
Видим, что первый эксперт не различил факторы по степени обладания признаком. В результате были определены связанные ранги, показанные в скобках. После экспертного оценивания была получена матрица размером п×т, где т - число экспертов, п - число объектов. Итоговая оценка каждого объекта получается суммированием рангов по столбцу:
|
Исходя из полученных результатов, можно провести вторичное ранжирование (предлагаем сделать это самостоятельно), при этом ранг 1 получит объект с минимальной Ri.
Напомним, что ранги объектов определяют только порядок расположения объектов по показателям сравнения (в данном случае - степени влияния на процесс обучения) и не дают ответа на вопрос о том, насколько или во сколько раз один лучше, чем другой. Достоинство метода – простота процедуры. Недостаток - невозможность упорядочить большое число объектов. Если оно превышает 20, то эксперты затрудняются в построении ранжированного ряда. Это объясняется тем, что при ранжировании эксперт должен рассматривать все объекты в их взаимосвязи как систему.
При увеличении числа объектов количество связей между ними растет весьма быстро, а удержание большого числа объектов и взаимосвязей в памяти ограничен психологическими возможностями людей.
Групповая оценка может быть признана удовлетворительной только при хорошей согласованности мнений опрашиваемых специалистов. Если разброс оценок велик, то следует выявить причины этого обстоятельства. Поэтому статистическая обработка информации, полученная от экспертов, должна включать в себя и оценку степени согласованности мнений экспертов.
|
|
|
|
|
|
Величина S имеет максимальное значение в случае когда все эксперты по каждому фактору выставили одинаковые ранги Исходя из этого, коэффициент конкордации W рассматривается как отношение фактически полученной величины S к ее максимальному значению Smax, зависящему от числа экспертов в группе т и числа факторов п, т.е. W=S/Smax.
Ясно что величина S может меняться от 1 до 0, причем равенство единице означает полное совпадение мнений экспертов (инаоборот).
Обычно W рассчитывается по так называемой формуле Кендалла:
W=12S/(m2(n3-n)).
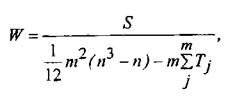 |
Эта формула справедлива, если все эксперты не выставили связанных рангов. В противном случае формула несколько усложняется:
|
где Tj= Σ(t3j - tj), а tj - число одинаковых рангов в j-м ряду.
Для оценки того факта, что совпадение мнений экспертов не случайно с определенной вероятностью, используется критерий Пирсона, подчиняющийся χ2 - распределению с числом степеней свободы
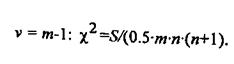
Если вычисленное значение χ2 будет больше табличного для соответствующего числа степеней свободы и значения доверительной вероятности (как правило, выбираемой на уровне 0,95-0,98), то считается, что групповому мнению экспертов можно доверять.
 |
В случае совпадения некоторых рангов χ2 определяется так:
Непосредственная оценка представляет собой процедуру приписывания объектам числовых значений в соответствующей шкале. Рассмотрим ее применение на примере метода «Дельфы», получившего название от греческого города «Дельфы», где был расположен знаменитый оракул древности - храм Аполлона и где прорицательница Пифия и жрецы предсказывали будущее путем толкования звуков и гула, доносившихся из расселины в скале, на которой стоял храм.
Метод представляет собой ряд последовательно осуществляемых процедур, которые характеризуются следующими основными чертами: анонимностью, информационной обратной связью и корректировкой групповой оценки на основе результатов каждого цикла обработки (как правило, не больше трех - четырех). Анонимность достигается тем, что каждый из экспертов не знает, кто еще участвует в экспертизе. Это является способом уменьшить влияние доминирующих экспертов на остальных, а, следовательно, и на результат. Информационная обратная связь осуществляется путем доведения до экспертов результатов обработки предыдущего этапа опроса без указания имен. Это позволяет экспертам заново взглянуть на свою оценку и либо приблизить ее к уточненной групповой, либо более тщательно обосновать свое особое мнение. Для осуществления экспертизы на основе дельфийского метода вопрос надо составить так, чтобы ответ можно было представить в виде числа. Следует также предоставить экспертам релевантную информацию. Рассмотрим процедуру метода на конкретном примере. Задача состояла в определении ожидаемого спроса на совершенно новую услугу. Применить один из известных методов планирования (нормативный, вычисления тренда или факторного анализа) нельзя по вполне понятным причинам - нет статистики. Экспертам было предложено предсказать спрос. При этом они получили информацию о том, каковы сегменты рынка, где предлагается позиционировать услугу, уровень потребления взаимозаменяющих услуг, а также использование этой услуги в других регионах (странах).
После первого тура опроса, результаты которого представлены в табл.4.2, аналитики провели статистическую обработку полученных данных.
Таблица 4.2
| Эксперты | |||||||
| Оценка опроса, Ед. |
Для этого оценки упорядочиваются, например, в порядке возрастания, как показано на рис. 4.1, а затем рассчитывают характеристики ряда: медиана и квартили. За медиану принимается средний член ряда, по отношению к которому число оценок справа и слева будет одинаковыми, что возможно при нечетном числе экспертов. При четном - за медиану выбирают середину интервала, делящего число оценок пополам. В нашем приме медиана совпала с оценкой 80 тыс. ед. Затем определяют верхний и нижний квартили как медианы нижней и верхней половин шкалы оценок. При этом интервал Q-Q2 считается наиболее предпочтительным.
После первого тура опроса экспертам сообщают значения медианы и квартилей. Экспертов, чьи оценки оказались за пределами Q1-Q2, просят мотивировать свое решение или пересмотреть с учетом новой информации. С полученными обоснованиями знакомят всех экспертов, не называя имени авторов. Такая процедура позволяет всем экспертам принять в расчете обстоятельства, которые они могли упустить из виду или о которых не знали во время первого тура опроса, и проставить новые оценки.
Результаты второго тура обрабатываются так же, как первого. Как правило, разброс оценок значения искомой величины уменьшается после второго тура, а после третьего практически перестает изменяться.
Улучшение групповой оценки в результате итерации основано на следующих предположениях:
• ответы экспертов, не изменяющих своих оценок, лежат ближе к истине, чем первоначальные оценки экспертов, не уверенных в своих ответах;
• среднее значение оценок экспертов, изменяющих ответы, движется в результате итераций к среднему уверенных экспертов, таким образом, групповая оценка улучшается.
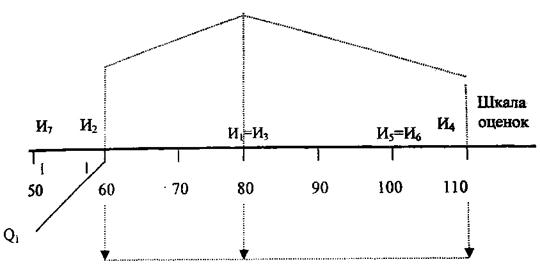
Рис. 4.1. Наиболее предпочтительные оценки
Практика применения метода показывает, что наличие в группе менее компетентных экспертов оказывает не столь значительное влияние на групповую оценку, чем простое усреднение оценок, поскольку итерации позволяют всем экспертам улучшить свое понимание проблемы за счет информации, получаемой от более компетентных специалистов. Кроме того, последние также не располагают всей информацией, которая имеется у всех входящих в группу, что позволяет и им улучшить свои оценки в ходе итерации.
Метод используется при прогнозировании на достаточно большом интервале времени, когда фактор неопределенности играет существенную роль. В сочетании с другими методами анализа ситуаций он может давать неоценимую информацию для принятия решений. Основной недостаток - длительность и высокая стоимость процедуры, а также невозможность прямого столкновения мнений экспертов, как при мозговом штурме.
Парное сравнение представляет собой процедуру установления предпочтений между объемами при сравнении всех возможных их пар. В отличие от ранжирования парное сравнение представляет значительно более простую задачу упорядочения объектов. При этом, оценивая каждую пару объектов Оi и Оj эксперт может установить, либо Оi предпочтительнее Оj либо Оj предпочтительнее Оi,либо они эквивалентны (Оi эквивалентен сам себе). При этом степень предпочтения может оцениваться по-разному. Например, в методе анализа иерархий, используется шкала от 1 до 9. Единица означает эквивалентность, а 9 очень высокую степень превосходства Оi над Оj. При этом Оj по отношению к Оi оценивается по принципу обратной симметрии, т.е. получает оценку 1/9. Каждый эксперт может давать свою матрицу оценок (попарных сравнений) или можно добиваться консенсуса в оценках, но полного упорядочения без специальных приемов метод попарного сравнения не дает.
Глава 5. СЕТЕВЫЕ МЕТОДЫ ПЛАНИРОВАНИЯ И УПРАВЛЕНИЯ
Дата добавления: 2015-04-16; просмотров: 260; Мы поможем в написании вашей работы!; Нарушение авторских прав |