Стабільне населення

Модель стабільного населення будується на припущенні, що щільність народжень змінюється, але при цьому протягом тривалого часу зберігається постійний режим відтворення населення. Передумови моделі стабільного населення такі:

1) постійний порядок вимирання, визначений показниками таблиці смертності;

2) зміна чисел народжених у геометричній прогресії;

3) відсутність зовнішньої міграції.

Як видно, на відміну від стабільного населення, гіпотеза постійності щільності народжень замінюється гіпотезою її постійної зміни у геометричній прогресії за формулою:

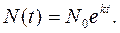(11.5)

Якщо у рік, прийнятий за початок періоду, народилося N₀, то в наступному році число народжених буде N₀ e^k. ще через рік – N₀ e^2k і т.д., а в попередні роки – N₀ e^-k, N₀ e^-2k і т.д. Із зазначеного видно, що числа народжених щорічно змінюються на одну і ту ж величину, а саме на e^k . Очевидно, що k представляє собою коефіцієнт природного приросту стабільного населення. Він називається коефіцієнтом прогресивності даного режиму відтворення населення або істинним коефіцієнтом природного приросту.

Якщо продовжити приклад, викладений для стаціонарного населення, то очевидно, що число 30-тирчних жінок буде дорівнювати . Але тут виникає питання про значення N: якого року треба взяти число народжених? Очевидно, що це мають бути народжені 20 років тому назад. Якщо визначати рік народження через t, то число народжених треба взяти для року (t-20), тобто N₀ e^k(t-20). Таким чином число жінок через 20 років після народження буде .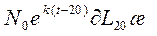

В цілому у віці х буде чоловіків і 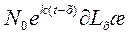жінок. Загальна чисельність населення у віці х складатиме:

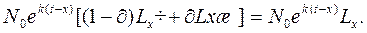(11.6)

Сума чисельності населення усіх вікових груп дасть нам загальну чисельність стабільного населення:

(11.7)

Як вже відмічалося, величина коефіцієнта прогресивності є постійна, а це означає, що при незмінному порядку вимирання населення, визначеного показниками таблиці смертності, значення коефіцієнта народжуваності залишається незмінним. Його можна визначити поділивши річне число народжень у році t, рівне 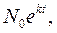на загальну чисельність стабільного населення (11.7):

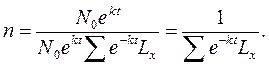(11.8)

Що стосується коефіцієнта природного приросту, то при зміні чисельності населення в геометричній прогресії він представляє собою натуральний логарифм її знаменника. Якщо знаменник прогресії e^k, то k і буде коефіцієнтом природного приросту. Значення коефіцієнта смертності можна розрахувати за формулою:

. (11.9)

Якщо виключити із формули чисельності населення 11.7 незалежний від віку х множник N₀e^kt, стане очевидним, що в стабільному населенні чисельність вікових груп пропорційна e^ktL_x. Це означає, що на відміну від стаціонарного населення чисельність груп стабільного населення пропорційна не тільки 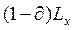і 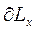, але й множнику e^-kt. Якщо 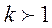, то цей множник з підвищенням віку зменшується. Позитивне k означає, що число народжень зростає. Чим вище вік, тим раніше народилися ті, хто знаходиться у цьому віці і тим меншим було їх число при народженні. Навпаки, якщо , число народжень скорочується, а e^-kt з підвищенням віку зростає. Це означає, що стабільне населення тем "молодше", чим вище коефіцієнт природного приросту, і навпаки.

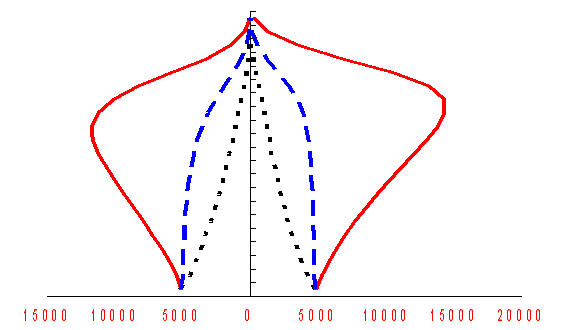
Рис. 11.1. Статево-вікова піраміда стабільних населень

На рисунку 11.1 наводиться статево-вікова піраміда для двох стабільних населень: з позитивним коефіцієнтом природного приросту k=0.02 і з від'ємним k= - 0,02. Відповідні знаменники геометричної прогресії складають e ^0,02=1,02 і e ^{– 0,02}=0,98.

Теорія стабільного населення показує обумовленість статево-вікової структури населення режимом його відтворення.

Моделі стаціонарного і стабільного населення, побудовані за наведеними вище гіпотезами, на перший погляд, ніяк не пов’язані з реальними обставинами формування його чисельності та статево-вікової структури, В той же час вони відіграють значну роль у демографічному аналізі. По-перше, порівняння фактичного населення з його теоретичними моделями дозволяє оцінити вплив компонентів відтворення населення (рівня народжуваності, порядку вимирання) на формування реальної структури. По-друге, моделі надають можливість представити структуру населення в майбутньому, якщо існуючий режим відтворення збережеться достатньо тривалий період часу.

Це особливо актуально зараз, коли в багатьох країнах вже відбувається процес стабілізації населення. Демографи прогнозують, що до середини нинішнього століття встановиться нульовий приріст населення, тобто його статево-вікова структура наблизиться до стаціонарної. Найвірогідніше, що це буде регресивний тип з високою часткою старших поколінь.

В Україні статево-вікова структура населення суттєво відрізняється від структури, заданої теоретичними моделями, що свідчить про складну демографічну історію, яку пережила наша країна у ХХ столітті.

Оскільки в основі побудови теоретичних моделей стаціонарного і стабільного населення лежать гіпотези, то моделі конкретного населення можуть бути побудовані в багатьох варіантах за різними заданими параметрами.

Запитання для самоконтролю

1. Необхідність побудови теоретичних моделей населення та їх роль в демографічному аналізі.

2. Гіпотези побудови моделі стаціонарного населення.

3. Порядок розрахунку параметрів стаціонарного населення.

4. Гіпотези побудови моделі стабільного населення.

5. Порядок розрахунку параметрів стабільного населення.

6. У чому полягає різниця між моделями стаціонарного і стабільного населення?

7. Поясніть поняття терміну "стабілізація населення".